
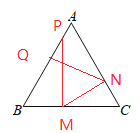
【题目】如图,在等边三角形ABC中,AB=5,在AB边上有一点P,过点P作PM⊥BC,垂足为M,过点M作MN⊥AC,垂足为N,过点N作NQ⊥AB,垂足为Q.当PQ=1时,BP=_____.
【答案】![]() 或
或![]()
【解析】由题意可知P点可能靠近B点,也可能靠近A点,所以需要分为两种情况:设BM=x,AQ=y,
若P靠近B点,由题意可得∠BPM=30°,根据直角三角形的性质可得BP=2BM=2x,AN=2y,CM=2CN=10-4y,再根据AB=BC=5,PQ=1,列方程组![]() ,解出x、y即可求得BP的长;
,解出x、y即可求得BP的长;
若点P靠近A点,同理可得![]() ,求解即可.
,求解即可.
设BM=x,AQ=y,
若P靠近B点,如图
∵等边△ABC,
∴AB=BC=AC=5,∠A=∠B=∠C=60°
∵PM⊥BC
∴∠BMP=90°
则Rt△BMP中,∠BPM=30°,
∴BM=![]() BP
BP
则BP=2x
同理AN=2y,
则CN=5-2y
在Rt△BCM中,CM=2CN=10-4y
∵AB=BC=5,PQ=1
∴![]()
解得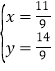
∴BP=2x=![]() ;
;
若点P靠近A点,如图
由上面的解答可得BP=2x,AQ=y,CM=10-4y
∴![]()
解得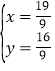
∴BP=2x=![]()
综上可得BP的长为:![]() 或
或![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“五一”期间,申老师一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数关系的图像.
(1)他们出发半小时后,离家多少千米?
(2)求出AB段的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家高斯在上学时曾经研究过这样一个问题,![]() ?
?
经过研究,这个问题的一般性结论是![]() ,其中
,其中![]() 为正整数,现在我们来研究一个类似的问题:
为正整数,现在我们来研究一个类似的问题:![]() ?
?
观察下面三个特殊的等式:
![]()
![]()
![]()
将这三个等式的两边相加,可以得到![]() .
.
读完这段材料,请你计算:
(1)![]() ________;(直接写出结果)
________;(直接写出结果)
(2)![]() ;(写出计算过程)
;(写出计算过程)
(3)![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别住在A、B、C三个住宅区,A区有25人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程总和最少,那么停靠点的位置应设在( )

A. A区 B. B区 C. A区或B区 D. C区
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,AB=AC,以AB为直径作⊙O,与BC交于点D,过D作AC的垂线,垂足为E.证明: 
(1)BD=DC;
(2)DE是⊙O切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
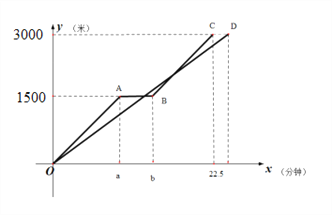
【题目】小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分)的关系如图所示,请结合图像,解答下列问题:
(1)a= b= ,m=
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com