
【题目】如图1,MN∥EF,C为两直线之间一点.
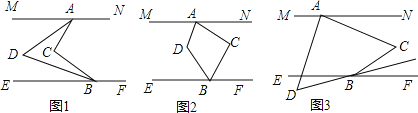
(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.
(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.
(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系: .
【答案】(1)∠ADB=50°;(2)∠ADB=180°﹣![]() ∠ACB;(3)∠ADB=90°﹣
∠ACB;(3)∠ADB=90°﹣![]() ACB.
ACB.
【解析】
试题分析:(1)如图1,根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG,根据角平分线的定义得到∠1=![]() ACG,∠2=
ACG,∠2=![]() ,即可得到结论;
,即可得到结论;
(2)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据角平分线的定义得到∠1=![]() ACG,∠2=
ACG,∠2=![]() ,根据平角的定义即可得到结论;
,根据平角的定义即可得到结论;
(3)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据平行线的定义得到∠1=![]() MAC,∠2=
MAC,∠2=![]() ∠CBF,根据四边形的内角和和角的和差即可得到结论.
∠CBF,根据四边形的内角和和角的和差即可得到结论.
解:(1)如图1,过C作CG∥MN,DH∥MN,
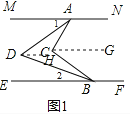
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠MAC=∠ACG,∠EBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴∠1=![]() ACG,∠2=
ACG,∠2=![]() ,
,
∴∠ADB=![]() (∠ACG+∠BCG)=
(∠ACG+∠BCG)=![]() ∠ACB;
∠ACB;
∵∠ACB=100°,
∴∠ADB=50°;
(2)如图2,过C作CG∥MN,DH∥MN,
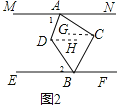
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴∠1=![]() ACG,∠2=
ACG,∠2=![]() ,
,
∴∠ADB=∠1+∠2=![]() (∠MAC+∠EBC)=
(∠MAC+∠EBC)=![]() (180°﹣∠NAC+180°﹣∠FBC)=
(180°﹣∠NAC+180°﹣∠FBC)=![]() (360°﹣∠ACB),
(360°﹣∠ACB),
∴∠ADB=180°﹣![]() ∠ACB;
∠ACB;
(3)如图3,过C作CG∥MN,DH∥MN,
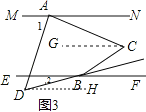
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠FBC的平分线相交于点D,
∴∠1=![]() MAC,∠2=
MAC,∠2=![]() ∠CBF,
∠CBF,
∵∠ADB=360°﹣∠1﹣(180°﹣∠2)﹣∠ACB=360°﹣![]() ∠MAC﹣(180°﹣
∠MAC﹣(180°﹣![]() ∠CBF)﹣∠ACB=360°﹣
∠CBF)﹣∠ACB=360°﹣![]() (180°﹣∠ACG)﹣(180°﹣
(180°﹣∠ACG)﹣(180°﹣![]() ∠BCG)=90°﹣
∠BCG)=90°﹣![]() ∠ACB.
∠ACB.
∴∠ADB=90°﹣![]() ACB.
ACB.
故答案为:∠ADB=90°﹣![]() ACB.
ACB.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
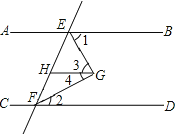
【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
(1)把下列证明过程及理由补充完整.
(2 )请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ( )
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+ =180° ( )
又∵EG平分∠BEF(已知)
∴∠1=![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2=![]() ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2=![]() ( + )
( + )
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
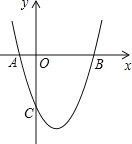
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果(x﹣2)(x﹣3)=x2+px+q,那么p、q的值是( )
A.p=﹣5,q=6
B.p=1,q=﹣6
C.p=1,q=6
D.p=﹣1,q=6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com