
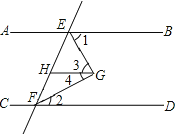
【题目】已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
(1)把下列证明过程及理由补充完整.
(2 )请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知)
∴∠1=∠3 ( )
又∵HG∥CD(已知)
∴∠2=∠4(同理)
∵AB∥CD(已知)
∴∠BEF+ =180° ( )
又∵EG平分∠BEF(已知)
∴∠1=![]() ∠
∠
又∵FG平分∠EFD(已知)
∴∠2=![]() ∠EFD (同理)
∠EFD (同理)
∴∠1+∠2=![]() ( + )
( + )
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°.
【答案】见解析
【解析】
试题分析:此题首先由平行线的性质得出∠1=∠3,∠2=∠4,∠BEF+∠EFD=180°,再由EG平分∠BEF,FG平分∠EFD得出∠1+∠2=90°,然后通过等量代换证出∠EGF=90°.
证明:∵HG∥AB(已知),
∴∠1=∠3,
又∵HG∥CD(已知),
∴∠2=∠4(两直线平行,内错角相等),
∵AB∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补),
又∵EG平分∠BEF(已知),
∴∠1=![]() ∠BEF(角平分线的定义),
∠BEF(角平分线的定义),
又∵FG平分∠EFD(已知),
∴∠2=![]() ∠EFD(角平分线的定义),
∠EFD(角平分线的定义),
∴∠1+∠2=![]() (∠BEF+∠EFD),
(∠BEF+∠EFD),
∴∠1+∠2=90°,
∴∠3+∠4=90°(等量代换)
即∠EGF=90°.
故答案为:两直线平行,内错角相等,∠EFD,两直线平行,同旁内角互补,角平分线的定义,EFD,∠BEF.两直线平行,内错角相等;
∠EFD; 两直线平行,同旁内角互补;
∠BEF;角平分线的定义;
∠BEF;∠EFD;
两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.


科目:初中数学 来源: 题型:
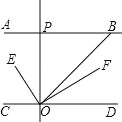
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=![]() °;
°;
②OF平分∠BOD;
③∠POE=∠BOF;
④∠POB=2∠DOF.
其中正确的个数有多少个?( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=﹣2×32 , b=(﹣2×3)2 , c=﹣(2×3)2 , 则下列大小关系中正确的是( )
A.a>b>c
B.b>c>a
C.b>a>c
D.c>a>b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线y=![]() x2+3x+1的一部分,如图所示.
x2+3x+1的一部分,如图所示.
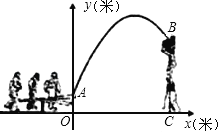
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,MN∥EF,C为两直线之间一点.
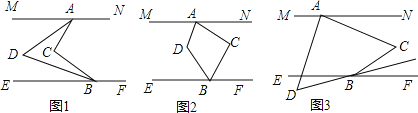
(1)如图1,若∠MAC与∠EBC的平分线相交于点D,若∠ACB=100°,求∠ADB的度数.
(2)如图2,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并证明你的结论.
(3)如图3,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请直接写出∠ACB与∠ADB之间的数量关系: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com