【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=40°，则下列结论：
①∠BOE=
°；
②OF平分∠BOD；
③∠POE=∠BOF；
④∠POB=2∠DOF．
其中正确的个数有多少个？（ ）
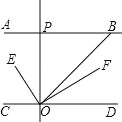
A．1 B．2 C．3 D．4
科目：初中数学 来源： 题型：
【题目】操作与证明：
如图1，已知P是矩形ABCD的边BC上的一个点（P与B、C两点不重合），过点P作射线PE⊥AP，在射线PE上截取线段PF，使得PF=AP．
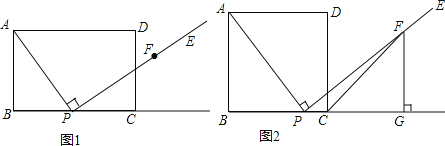
（1）过点F作FG⊥BC交射线BC点G．（尺规作图，保留痕迹，不写作法）
（2）求证：FG=BP．
探究与计算：
（3）如图2，若AB=BC，连接CF，求∠FCG的度数；
（4）在（3）的条件下，当
=
时，求sin∠CFP的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1=∠2，求证：CD⊥AB．
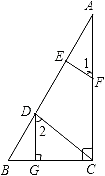
证明：∵DG⊥BC，AC⊥BC（已知）
∴∠DGB=∠ACB=90°（垂直定义）
∴DG∥AC（ ）
∴∠2= （ ）
∵∠1=∠2（已知）
∴∠1=∠ （等量代换）
∴EF∥CD（ ）
∴∠AEF=∠ （ ）
∵EF⊥AB（已知）
∴∠AEF=90°（ ）
∴∠ADC=90°（ ）
∴CD⊥AB（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，AB∥CD∥GH，EG平分∠BEF，FG平分∠EFD
求证：∠EGF=90°
（1）把下列证明过程及理由补充完整．
（2 ）请你用精炼准确的文字将上述结论总结出来．
证明：∵HG∥AB（已知）
∴∠1=∠3 （ ）
又∵HG∥CD（已知）
∴∠2=∠4（同理）
∵AB∥CD（已知）
∴∠BEF+ =180° （ ）
又∵EG平分∠BEF（已知）
∴∠1=
∠
又∵FG平分∠EFD（已知）
∴∠2=∠EFD （同理）
∴∠1+∠2=（ + ）
∴∠1+∠2=90°
∴∠3+∠4=90°
即∠EGF=90°．
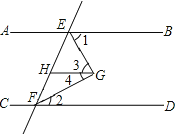
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
