
【题目】操作与证明:
如图1,已知P是矩形ABCD的边BC上的一个点(P与B、C两点不重合),过点P作射线PE⊥AP,在射线PE上截取线段PF,使得PF=AP.
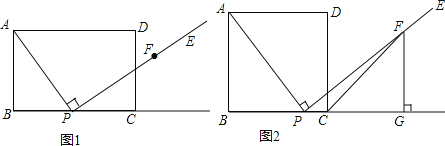
(1)过点F作FG⊥BC交射线BC点G.(尺规作图,保留痕迹,不写作法)
(2)求证:FG=BP.
探究与计算:
(3)如图2,若AB=BC,连接CF,求∠FCG的度数;
(4)在(3)的条件下,当![]() =
=![]() 时,求sin∠CFP的值.
时,求sin∠CFP的值.
【答案】(1)见解析;(2)见解析;(3)∠FCG=45°;(4)![]() .
.
【解析】
试题分析:(1)利用作一个角等于已知角的方法,即可作出所求直线;
(2)易求得∠BAP=∠GPF,∠ABP=∠PGF=90°,又由AP=PF,即可证得△ABP≌△PGF,继而证得结论;
(3)首先证得FG=CG,即可得△FCG是等腰直角三角形,继而求得答案;
(4)首先作CH⊥PF于H,易证得△PHC∽△PGF,由相似三角形的对应边成比例,可得![]() ,然后设BP=3a,则PC=a,PG=4a,FG=CG=3a,分别求得FC,HC,继而求得答案.
,然后设BP=3a,则PC=a,PG=4a,FG=CG=3a,分别求得FC,HC,继而求得答案.
(1)解:如图1所示:
(2)证明:∵PE⊥AP,
∴∠APE=90°.
∴∠APB+∠GPF=90°,
又∵∠APB+∠BAP=90°,
∴∠BAP=∠GPF,
又∵FG⊥BC,
∴∠ABP=∠PGF=90°,
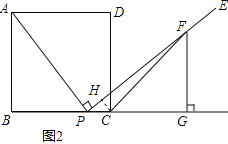
在△ABP与△PGF中,
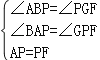 ,
,
∴△ABP≌△PGF(AAS).
∴FG=BP;
(3)解:由(2)知AB=PG,
∵AB=BC,
∴BC=PG.
∴BC﹣PC=PG﹣PC.
∴BP=CG,
又∵FG=BP,
∴FG=CG.
又∵∠CGF=90°,
∴∠FCG=45°;
(4)解:如图2,作CH⊥PF于H,
∵∠HPC=∠GPF,∠CHP=∠FGP=90°,
∴△PHC∽△PGF.
∴![]() ,
,
根据![]() ,
,
设BP=3a,则PC=a,PG=4a,FG=CG=3a,
∴PF=![]() =5a,CF=
=5a,CF=![]() =3
=3![]() a,
a,
∴![]() .
.
∴HC=![]() a,
a,
∴sin∠CFP= =
=![]() .
.



 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列选项中,具有相反意义的量是( )
A.收入20元与支出30元
B.上升了6米和后退了7米
C.卖出10斤米和盈利10元
D.向东行30米和向北行30米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A(-3,y1)、B(0,y2)是二次函数y=-2(x-1)2+3图象上的两点,那么y1与y2的大小关系是________(填y1>y2、y1=y2或y1<y2).
查看答案和解析>>
科目:初中数学 来源: 题型:
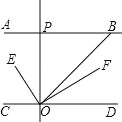
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=![]() °;
°;
②OF平分∠BOD;
③∠POE=∠BOF;
④∠POB=2∠DOF.
其中正确的个数有多少个?( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com