[题目]如图.长方体的长为.宽为.高为.点离点的距离为.一只蚂蚁如果要沿着长方体的表面从点爬到点.需要爬行的最短距离是( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，长方体的长为，宽为，高为，点离点的距离为，一只蚂蚁如果要沿着长方体的表面从点爬到点，需要爬行的最短距离是（）

A.B.C.D.

【答案】B

【解析】

将长方体侧表面剪开与前面、上面、后面侧面分别形成一个长方形，分别利用勾股定理计算出AB的距离即可解答.

只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如图1：

因为长方体的宽为10，高为20，点B离点C的距离为5，

所以BD=CD+BC=10+5=15，AD=20

在直角三角形ABD中，根据勾股定理得：

只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图2：

此时BD=CD+BC=20+5=25,所以

同理与后面侧面所在构成一个长方形，如图3，

可求

因为

所以选B.

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（0，-1）．

（1）画出△ABC关于原点O成中心对称的图形△A1B1C1；

（2）在（1）的条件下直接写出点A1的坐标为______；B1的坐标为______；

（3）求出△ABC的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，正方形ABCD中，E为BC上一点，AF平分∠DAE，求证：BE+DF=AE.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】根据道路管理规定，在贺州某段笔直公路上行驶的车辆，限速千米/时，已知交警测速点到该公路点的距离为米，，（如图所示），现有一辆汽车由往方向匀速行驶，测得此车从点行驶到点所用的时间为秒．

求测速点到该公路的距离；

通过计算判断此车是否超速．（参考数据：，，）

查看答案和解析>>

科目：初中数学 来源： 题型：

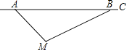
【题目】如图所示，△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD．

（1）用尺规作图的方法，过D点作DM⊥BE，垂足是M（不写作法，保留作图痕迹）；

（2）求证：BM=EM．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知二次函数的图象如图，下列结论：①；②；③；④；⑤，正确的个数是（）

A. 4个 B. 3个 C. 2个 D. 1个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读理解与应用:对式子x2+2x－3变形如下：x2+2x－3=x2+2x+1－1－3=(x2+2x+1)－4=(x+1)2－4．像这种变形抓住了完全平方公式的特点，先在原式中添加一项，使其中的三项成为完全平方式，再减去添加的这项，我们把这种恒等变形叫配方. 配方法是一种用来把二次多项式化为一个一次多项式的平方与一个常数的和的方法，它的应用十分广泛.请你尝试解决下列问题：

(1)对式子x2－2x+2020进行配方；

(2)已知2y－2x2－8x=y+10，求y的最小值；

(3)如图，在足够大的空地上有一段长为a(a≥250)米的旧墙MN，某人利用旧墙和木栏围成一个长方形菜园ABCD，其中 AD≤MN，已知长方形菜园的一边靠墙，另三边一共用了100米木栏. 求长方形菜园ABCD面积的最大值．