
ЁОЬтФПЁПдФЖСРэНтгыгІгУ:ЖдЪНзгx2+2xЃ3БфаЮШчЯТЃКx2+2xЃ3=x2+2x+1Ѓ1Ѓ3=(x2+2x+1)Ѓ4=(x+1)2Ѓ4ЃЎЯёетжжБфаЮзЅзЁСЫЭъШЋЦНЗНЙЋЪНЕФЬиЕуЃЌЯШдкдЪНжаЬэМгвЛЯюЃЌЪЙЦфжаЕФШ§ЯюГЩЮЊЭъШЋЦНЗНЪНЃЌдйМѕШЅЬэМгЕФетЯюЃЌЮвУЧАбетжжКуЕШБфаЮНаХфЗН. ХфЗНЗЈЪЧвЛжжгУРДАбЖўДЮЖрЯюЪНЛЏЮЊвЛИівЛДЮЖрЯюЪНЕФЦНЗНгывЛИіГЃЪ§ЕФКЭЕФЗНЗЈЃЌЫќЕФгІгУЪЎЗжЙуЗК.ЧыФуГЂЪдНтОіЯТСаЮЪЬтЃК
(1)ЖдЪНзгx2Ѓ2x+2020НјааХфЗНЃЛ
(2)вбжЊ2yЃ2x2Ѓ8x=y+10ЃЌЧѓyЕФзюаЁжЕЃЛ
(3)ШчЭМЃЌдкзуЙЛДѓЕФПеЕиЩЯгавЛЖЮГЄЮЊa(aЁн250)УзЕФОЩЧНMNЃЌФГШЫРћгУОЩЧНКЭФОРИЮЇГЩвЛИіГЄЗНаЮВЫдАABCDЃЌЦфжа ADЁмMNЃЌвбжЊГЄЗНаЮВЫдАЕФвЛБпППЧНЃЌСэШ§БпвЛЙВгУСЫ100УзФОРИ. ЧѓГЄЗНаЮВЫдАABCDУцЛ§ЕФзюДѓжЕЃЎ

ЁОД№АИЁП(1) (x-1)2+2019ЃЛ(2) yЕФзюаЁжЕЮЊ2ЃЛ(3) ГЄЗНаЮВЫдАABCDУцЛ§ЕФзюДѓжЕЮЊ1250ЦНЗНУз.
ЁОНтЮіЁП
(1)ИљОнВФСЯжаИјГіЕФХфЗНЗЈНјааХфЗНМДПЩЧѓЕУД№АИЃЛ
(2)ЯШгУКЌxЕФЪНзгБэЪОyЃЌШЛКѓИљОнХфЗНЗЈЕУЕНy=2(x-2)2+2ЃЌдйИљОнЦНЗНЕФЗЧИКадМДПЩЧѓЕУД№АИЃЛ
(3)ЩшABЮЊxЃЌГЄЗНаЮЕФУцЛ§ЮЊSЃЌИљОнГЄЗНаЮУцЛ§ЙЋЪНСаГіSгыxЕФЙиЯЕЃЌМЬЖјРћгУХфЗНЗЈНјааЧѓНтМДПЩ.
(1) x2Ѓ2x+2020
=x2-2x+1-1+2020
=(x-1)2+2019ЃЛ
(2) 2yЃ2x2Ѓ8x=y+10ЃЌ
2y-y=2x2-8x-10ЃЌ
y=2(x2-4x+4-4)+10
=2(x-2)2+2ЃЌ
Ёп(x-2)2Ён0ЃЌ
Ёрy=2(x-2)2+2Ён2ЃЌ
ЁрyЕФзюаЁжЕЮЊ2ЃЛ
(3) ЩшABЮЊxЃЌГЄЗНаЮЕФУцЛ§ЮЊSЃЌдђга
S=x(100-2x)
=-2x2+100x
=-2(x2-50x+625-625)
=-2(x-25)2+1250ЃЌ
вђЮЊ(x-25)2Ён0ЃЌ
Ыљвд-2(x-25)2Ём0ЃЌ
ЫљвдS=-2(x-25)2+1250Ём1250ЃЌ
МДГЄЗНаЮВЫдАABCDУцЛ§ЕФзюДѓжЕЮЊ1250ЦНЗНУз.


 ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
ССЕуМЄЛюОЋБрЬсгХ100ЗжДѓЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃКдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЫФБпаЮOABCЪЧГЄЗНаЮЃЌЕуAЁЂCЁЂDЕФзјБъЗжБ№ЮЊAЃЈ9ЃЌ0ЃЉЁЂCЃЈ0ЃЌ4ЃЉЃЌDЃЈ5ЃЌ0ЃЉЃЌЕуPДгЕуOГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиOЁњCЁњBЁњAдЫЖЏЃЌЕуPЕФдЫЖЏЪБМфЮЊtУы.
ЃЈ1ЃЉЕБt=5ЪБЃЌ OPГЄЮЊ____________ЃЛ
ЃЈ2ЃЉЕБЕуPдкBCБпЩЯЪБЃЌOP+PDгазюаЁжЕТ№ЃПШчЙћгаЃЌЧыЫуГіИУзюаЁжЕЃЌШчЙћУЛгаЃЌЧыЫЕУїРэгЩЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊAЁЂBЁЂCЁЂDЫФЕуЕФзјБъвРДЮЮЊЃЈ0ЃЌ0ЃЉЁЂЃЈ6ЃЌ0ЃЉЃЈ8ЃЌ6ЃЉЁЂЃЈ2ЃЌ6ЃЉЃЌШєвЛДЮКЏЪ§y=mxЉ6mЕФЭМЯѓНЋЫФБпаЮABCDЕФУцЛ§ЗжГЩ1ЃК3СНВПЗжЃЌдђmЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌГЄЗНЬхЕФГЄЮЊ![]() ЃЌПэЮЊ
ЃЌПэЮЊ![]() ЃЌИпЮЊ
ЃЌИпЮЊ![]() ЃЌЕу
ЃЌЕу![]() РыЕу
РыЕу![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌвЛжЛТьвЯШчЙћвЊбизХГЄЗНЬхЕФБэУцДгЕу
ЃЌвЛжЛТьвЯШчЙћвЊбизХГЄЗНЬхЕФБэУцДгЕу![]() ХРЕНЕу
ХРЕНЕу![]() ЃЌашвЊХРааЕФзюЖЬОрРыЪЧЃЈ ЃЉ
ЃЌашвЊХРааЕФзюЖЬОрРыЪЧЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќШ§НЧаЮABCЕзБпBCЕФГЄЮЊ4ЃЌУцЛ§ЮЊ12ЃЌбќABЕФДЙжБЦНЗжЯпEFНЛABгкЕуEЃЌНЛACгкЕуF.ШєDЮЊBCБпЕФжаЕуЃЌMЮЊЯпЖЮEFЩЯвЛИіЖЏЕуЃЌдђЁїBDMЕФжмГЄЕФзюаЁжЕЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыКЏЪ§y=x-![]() ЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйab>0ЃЛЂкc>-
ЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйab>0ЃЛЂкc>-![]() ЃЛЂлa+b+c<-
ЃЛЂлa+b+c<-![]() ЃЛЂмЗНГЬax2+ЃЈb-1ЃЉx+c+
ЃЛЂмЗНГЬax2+ЃЈb-1ЃЉx+c+![]() =0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎЦфжае§ШЗЕФга( )
=0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎЦфжае§ШЗЕФга( )
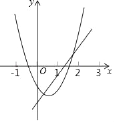
A. 4Иі B. 3Иі C. 2Иі D. 1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
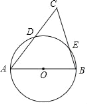
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCЪЧЁбOЭтвЛЕуЃЌACЃЌBCЗжБ№гыЁбOЯрНЛгкDЃЎ
ЃЈ1ЃЉдкЭМжазїГіЁїABCЕФБпABЩЯЕФИпCHЃЎЃЈвЊЧѓЃКЂйНігУЮоПЬЖШецГпЃЌЧвВЛФмгУжБГпжаЕФжБНЧЃЛЂкБЃСєБивЊЕФзїЭМКлМЃЃЉ
ЃЈ2ЃЉСЌНгDEЃЌШє![]() ЃЌдђЁЯCЕФЖШЪ§ЪЧЁЁЁЁЃЎ
ЃЌдђЁЯCЕФЖШЪ§ЪЧЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
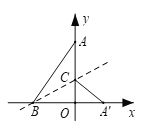
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈ0ЃЌ12ЃЉЃЌBЃЈЃ5ЃЌ0ЃЉЃЌСЌНгABЃЎНЋЁїAOBбиЙ§ЕуBЕФжБЯпелЕўЃЌЪЙЕуAТфдкxжсЩЯЕФЕу![]() ДІЃЌелКлЫљдкЕФжБЯпНЛyжсе§АыжсгкЕуCЃЌдђЕуCЕФзјБъЮЊ___________________________.
ДІЃЌелКлЫљдкЕФжБЯпНЛyжсе§АыжсгкЕуCЃЌдђЕуCЕФзјБъЮЊ___________________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЕФШ§ИіЖЅЕудкБпГЄЮЊ1ЕФе§ЗНаЮЭјИёжаЃЌвбжЊ
ЕФШ§ИіЖЅЕудкБпГЄЮЊ1ЕФе§ЗНаЮЭјИёжаЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .
.
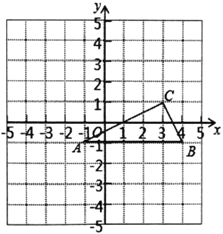
(1)ЛГі![]() Йигк
Йигк![]() жсЖдГЦЕФ
жсЖдГЦЕФ![]() (Цфжа
(Цфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЖдгІЕуЃЌВЛаДЛЗЈ)ЃЛ
ЕФЖдгІЕуЃЌВЛаДЛЗЈ)ЃЛ
(2)ЗжБ№аДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЕФзјБъ.
Ш§ЕуЕФзјБъ.
(3)ЧыаДГіЫљгавд![]() ЮЊБпЧвгы
ЮЊБпЧвгы![]() ШЋЕШЕФШ§НЧаЮЕФЕкШ§ИіЖЅЕу(ВЛгы
ШЋЕШЕФШ§НЧаЮЕФЕкШ§ИіЖЅЕу(ВЛгы![]() жиКЯ)ЕФзјБъ_____.
жиКЯ)ЕФзјБъ_____.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com