
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.
(1)当t=5时, OP长为____________;
(2)当点P在BC边上时,OP+PD有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
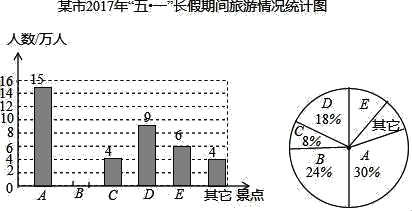
【题目】随着道路交通的不断完善,某市旅游业快速发展,该市旅游景区有A、B、C、D、E等著名景点,市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图(不完整)如下所示,根据相关信息解答下列问题:
(1)2017年“五一”期间,该市旅游景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)在等可能性的情况下,甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少?请用画树状图或列表加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).
(1)画出△ABC关于原点O成中心对称的图形△A1B1C1;
(2)在(1)的条件下直接写出点A1的坐标为______;B1的坐标为______;
(3)求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年南宁市地铁
年南宁市地铁![]() 号线二期工程建设如火如荼.预计
号线二期工程建设如火如荼.预计![]() 年底投入运营,从此省城南宁市将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工
年底投入运营,从此省城南宁市将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工![]() 天完成该项工程的
天完成该项工程的![]() ,这时乙队加入,两队还需同时施工
,这时乙队加入,两队还需同时施工![]() 天才能完成该项工程.
天才能完成该项工程.
![]() 若乙队单独施工,需要多少天才能完成该项工程?
若乙队单独施工,需要多少天才能完成该项工程?
![]() 若甲队参与该项工程施工的时间不超过
若甲队参与该项工程施工的时间不超过![]() 天,则乙队至少施工多少天才能完成该项工程?
天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距120km,甲、乙两人从两地出发相向而行,甲先出发.图中
两地相距120km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() (km)与时间 (h)的关系,结合图像回答下列问题:
(km)与时间 (h)的关系,结合图像回答下列问题:
(1)表示乙离开![]() 地的距离与时间关系的图像是 (填
地的距离与时间关系的图像是 (填![]() 或
或![]() );
);
甲的速度是 km/h,乙的速度是 km/h.
(2)何时两人在途中相遇?
(3)甲出发后多少时间两人恰好相距10km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解与应用:对式子x2+2x-3变形如下:x2+2x-3=x2+2x+1-1-3=(x2+2x+1)-4=(x+1)2-4.像这种变形抓住了完全平方公式的特点,先在原式中添加一项,使其中的三项成为完全平方式,再减去添加的这项,我们把这种恒等变形叫配方. 配方法是一种用来把二次多项式化为一个一次多项式的平方与一个常数的和的方法,它的应用十分广泛.请你尝试解决下列问题:
(1)对式子x2-2x+2020进行配方;
(2)已知2y-2x2-8x=y+10,求y的最小值;
(3)如图,在足够大的空地上有一段长为a(a≥250)米的旧墙MN,某人利用旧墙和木栏围成一个长方形菜园ABCD,其中 AD≤MN,已知长方形菜园的一边靠墙,另三边一共用了100米木栏. 求长方形菜园ABCD面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com