
【题目】如图,点B(3,3)在双曲线y=![]() (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣![]() (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(1)求k的值;
(2)求点A的坐标.

【答案】(1)9.(2)(1,0).
【解析】试题分析:(1)、将点B代入反比例函数解析式求出k的值;(2)、设MD=a,OM=b,从而得出ab=4,过D作DM⊥x轴于M,过B作BN⊥x轴于N,则∠DMA=∠ANB=90°,根据正方形的性质得出△ADM和△BAN全等,从而得出BN=AM=3,DM=AN=a,0A=3﹣a,即AM=b+3﹣a=3,a=b,根据ab=4得出a=b=2,从而得出OA=1,从而求出点A的坐标.
试题解析:(1)、∵点B(3,3)在双曲线y=![]() 上,∴k=3×3=9;
上,∴k=3×3=9;
(2)、∵B(3,3),∴BN=ON=3,设MD=a,OM=b,∵D在双曲线y=![]() (x<0)上,∴ab=4
(x<0)上,∴ab=4
过D作DM⊥x轴于M,过B作BN⊥x轴于N,则∠DMA=∠ANB=90°
∵四边形ABCD是正方形,∴∠DAB=90°,AD="AB" ∴∠MDA+∠DAM=90°,∠DAM+∠BAN=90°,∴∠ADM=∠BAN
在△ADM和△BAN中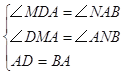 ∴△ADM≌△BAN ∴BN=AM=3,DM=AN=a,∴0A=3﹣a,
∴△ADM≌△BAN ∴BN=AM=3,DM=AN=a,∴0A=3﹣a,
即AM=b+3﹣a=3,a=b, ∵ab=4,∴a=b=2,∴OA=3﹣2=1, 即点A的坐标是(1,0)


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=![]() .
.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明做了以下5道题:①(x﹣1)(x+4)=x2﹣4;②(﹣3+x)(3+x)=x2﹣9;③(﹣5x+7y)(﹣5x﹣7y)=25x2﹣49y2;④(xy﹣6)2=x2y2﹣12xy+36;⑤(﹣x﹣y)2=x2+2xy+y2 , 你认为小明一共做对了( )
A.5道
B.4道
C.3道
D.2道
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台.若商店保持两种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】餐桌边的一蔬一饭,舌尖上的一饮一酌,实属来之不易,舌尖上的浪费让人触目惊心.据统计,中国每年浪费的食物总量折合粮食约500亿千克,这个数据用科学记数法表示为( )
A.5×109千克 B.50×109千克
C.5×1010千克 D.0.5×1011千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长都为整数的△ABC≌△DEF ,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为( )
A.3
B.4
C.5
D.3或4或5
查看答案和解析>>
科目:初中数学 来源: 题型:
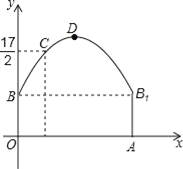
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com