
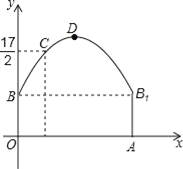
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
【答案】(1)拱顶D到地面OA的距离为10m;(2)这辆货车能安全通过;(3)两排灯的水平距离最小是4![]() m.
m.
【解析】试题分析:(1)先确定B点和C点坐标,然后利用待定系数法求出抛物线解析式,再利用配方法确定顶点D的坐标,从而得到点D到地面OA的距离;
(2)由于抛物线的对称轴为直线x=6,而隧道内设双向行车道,车宽为4m,则货运汽车最外侧与地面OA的交点为(2,0)或(10,0),然后计算自变量为2或10的函数值,再把函数值与6进行大小比较即可判断;
(3)抛物线开口向下,函数值越大,对称点之间的距离越小,于是计算函数值为8所对应的自变量的值即可得到两排灯的水平距离最小值.
解:(1)根据题意得B(0,4),C(3,![]() ),
),
把B(0,4),C(3,![]() )代入y=﹣
)代入y=﹣![]() x2+bx+c得
x2+bx+c得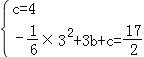 ,
,
解得![]() .
.
所以抛物线解析式为y=﹣![]() x2+2x+4,
x2+2x+4,
则y=﹣![]() (x﹣6)2+10,
(x﹣6)2+10,
所以D(6,10),
所以拱顶D到地面OA的距离为10m;
(2)由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=![]() >6,
>6,
所以这辆货车能安全通过;
(3)令y=8,则﹣![]() (x﹣6)2+10=8,解得x1=6+2
(x﹣6)2+10=8,解得x1=6+2![]() ,x2=6﹣2
,x2=6﹣2![]() ,
,
则x1﹣x2=4![]() ,
,
所以两排灯的水平距离最小是4![]() m.
m.


科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线y=![]() (x>0)上,点D在双曲线y=﹣
(x>0)上,点D在双曲线y=﹣![]() (x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(x<0)上,点A和点C分别在x轴、y轴的正半轴上,且点A、B、C构成的四边形为正方形
(1)求k的值;
(2)求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电影《流浪地球》中有一个名词“洛希极限”,它是指两大星体之间可以保持平稳运行的最小距离,其中地球与木星之间的洛希极限约为10.9万公里,数据“10.9万”用科学记数法表示正确的是( )
A. 10.9×104B. 1.09×104C. 10.9×105D. 1.09×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
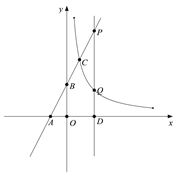
如图,在平面直角坐标系xoy中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线![]() 在第一象限内交于点C(1,m).
在第一象限内交于点C(1,m).
(1)求![]() 和
和![]() 的值;
的值;
(2)过![]() 轴上的点D(
轴上的点D(![]() ,0)作平行于y轴的直线
,0)作平行于y轴的直线![]() (
(![]() ),分别与直线AB和双曲线
),分别与直线AB和双曲线![]() 交于点P、Q,且PQ=2QD,求△APQ的面积.
交于点P、Q,且PQ=2QD,求△APQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的作业本上有四道利用不等式的性质,将不等式化为x>a或x<a的作业题:①由x+7>8解得x>1;②由x<2x+3解得x<3;③由3x-1>x+7解得x>4;④由-3x>-6解得x<-2.其中正确的有( )
A. 1题 B. 2题
C. 3题 D. 4题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com