
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨ő“√«∂®“Ś÷ĪŌŖy=ax©Āaő™Ň◊őÔŌŖ![]() £®a°Ęb°Ęcő™≥£ ż£¨a°Ŕ0£©Ķń°į√őŌŽ÷ĪŌŖ°Ī£Ľ”–“ĽłŲ∂•Ķ„‘ŕŇ◊őÔŌŖ…Ō£¨ŃŪ”–“ĽłŲ∂•Ķ„‘ŕy÷Š…ŌĶń»żĹ«–őő™∆š°į√őŌŽ»żĹ«–ő°Ī£ģ
£®a°Ęb°Ęcő™≥£ ż£¨a°Ŕ0£©Ķń°į√őŌŽ÷ĪŌŖ°Ī£Ľ”–“ĽłŲ∂•Ķ„‘ŕŇ◊őÔŌŖ…Ō£¨ŃŪ”–“ĽłŲ∂•Ķ„‘ŕy÷Š…ŌĶń»żĹ«–őő™∆š°į√őŌŽ»żĹ«–ő°Ī£ģ

“—÷™Ň◊őÔŌŖ![]() ”Ž∆š°į√őŌŽ÷ĪŌŖ°ĪĹĽ”ŕA°ĘBŃĹĶ„£®Ķ„A‘ŕĶ„BĶń◊ů≤ŗ£©£¨”Žx÷ŠłļįŽ÷ŠĹĽ”ŕĶ„C£ģ
”Ž∆š°į√őŌŽ÷ĪŌŖ°ĪĹĽ”ŕA°ĘBŃĹĶ„£®Ķ„A‘ŕĶ„BĶń◊ů≤ŗ£©£¨”Žx÷ŠłļįŽ÷ŠĹĽ”ŕĶ„C£ģ
£®1£©ŐÓŅ’£ļł√Ň◊őÔŌŖĶń°į√őŌŽ÷ĪŌŖ°ĪĶńĹ‚őŲ Ĺő™ £¨Ķ„AĶń◊ÝĪÍő™ £¨Ķ„BĶń◊ÝĪÍő™ £Ľ
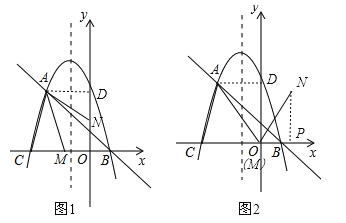
£®2£©»ÁÕľ£¨Ķ„Mő™ŌŖ∂őCB…Ō“Ľ∂ĮĶ„£¨Ĺę°ųACM“‘AMňý‘ŕ÷ĪŌŖő™∂‘≥∆÷Š∑≠’Ř£¨Ķ„CĶń∂‘≥∆Ķ„ő™N£¨»Ű°ųAMNő™ł√Ň◊őÔŌŖĶń°į√őŌŽ»żĹ«–ő°Ī£¨«ůĶ„NĶń◊ÝĪÍ£Ľ
£®3£©ĶĪĶ„E‘ŕŇ◊őÔŌŖĶń∂‘≥∆÷Š…Ō‘ň∂Į Ī£¨‘ŕł√Ň◊őÔŌŖĶń°į√őŌŽ÷ĪŌŖ°Ī…Ō£¨ «∑Ůīś‘ŕĶ„F£¨ ĻĶ√“‘Ķ„A°ĘC°ĘE°ĘFő™∂•Ķ„ĶńňńĪŖ–őő™∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ£¨«Ž÷ĪĹ”–ī≥ŲĶ„E°ĘFĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©![]() £Ľ£®©Ā2£¨
£Ľ£®©Ā2£¨ ![]() £©£Ľ£®1£¨0£©£Ľ£®2£©NĶ„◊ÝĪÍő™£®0£¨
£©£Ľ£®1£¨0£©£Ľ£®2£©NĶ„◊ÝĪÍő™£®0£¨ ![]() ©Ā3£©ĽÚ£®
©Ā3£©ĽÚ£®![]() £¨
£¨ ![]() £©£Ľ£®3£©E£®©Ā1£¨©Ā
£©£Ľ£®3£©E£®©Ā1£¨©Ā![]() £©°ĘF£®0£¨
£©°ĘF£®0£¨ ![]() £©ĽÚE£®©Ā1£¨©Ā
£©ĽÚE£®©Ā1£¨©Ā![]() £©°ĘF£®©Ā4£¨
£©°ĘF£®©Ā4£¨ ![]() £©£ģ
£©£ģ
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©”…√őŌŽ÷ĪŌŖĶń∂®“ŚŅ…«ůĶ√∆šĹ‚őŲ Ĺ£¨Ń™ŃĘ√őŌŽ÷ĪŌŖ”ŽŇ◊őÔŌŖĹ‚őŲ ĹŅ…«ůĶ√A°ĘBĶń◊ÝĪÍ£Ľ
£®2£©ĶĪNĶ„‘ŕy÷Š…Ō Ī£¨ĻżA◊ųAD°Õy÷Š”ŕĶ„D£¨‘ÚŅ…÷™AN=AC£¨ĹŠļŌAĶ„◊ÝĪÍ£¨‘ÚŅ…«ůĶ√ONĶń≥§£¨Ņ…«ůĶ√NĶ„◊ÝĪÍ£ĽĶĪMĶ„‘ŕy÷Š…ŌľīMĶ„‘ŕ‘≠Ķ„ Ī£¨ĻżN◊ųNP°Õx÷Š”ŕĶ„P£¨”…ŐűľĢŅ…«ůĶ√°ŌNMP=60°„£¨‘ŕRt°ųNMP÷–£¨Ņ…«ůĶ√MPļÕNPĶń≥§£¨‘ÚŅ…«ůĶ√NĶ„◊ÝĪÍ£Ľ
£®3£©ĶĪACő™∆Ĺ––ňńĪŖ–őĶń“ĽĪŖ Ī£¨ĻżF◊ų∂‘≥∆÷ŠĶńīĻŌŖFH£¨ĻżA◊ųAK°Õx÷Š”ŕĶ„K£¨Ņ…÷§°ųEFH°’°ųACK£¨Ņ…«ůĶ√DFĶń≥§£¨‘ÚŅ…«ůĶ√FĶ„ĶńļŠ◊ÝĪÍ£¨ī”∂ÝŅ…«ůĶ√FĶ„◊ÝĪÍ£¨”…HEĶń≥§Ņ…«ůĶ√EĶ„◊ÝĪÍ£ĽĶĪACő™∆Ĺ––ňńĪŖ–őĶń∂‘Ĺ«ŌŖ Ī£¨…ŤE£®©Ā1£¨t£©£¨”…A°ĘCĶń◊ÝĪÍŅ…ĪŪ ĺ≥ŲAC÷–Ķ„£¨ī”∂ÝŅ…ĪŪ ĺ≥ŲFĶ„Ķń◊ÝĪÍ£¨īķ»Ž÷ĪŌŖABĶńĹ‚őŲ ĹŅ…«ůĶ√tĶń÷Ķ£¨Ņ…«ůĶ√E°ĘFĶń◊ÝĪÍ£ģ
£®1£©°ŖŇ◊őÔŌŖ![]() £¨°ŗ∆š√őŌŽ÷ĪŌŖĶńĹ‚őŲ Ĺő™
£¨°ŗ∆š√őŌŽ÷ĪŌŖĶńĹ‚őŲ Ĺő™![]() £¨Ń™ŃĘ√őŌŽ÷ĪŌŖ”ŽŇ◊őÔŌŖĹ‚őŲ ĹŅ…Ķ√£ļ
£¨Ń™ŃĘ√őŌŽ÷ĪŌŖ”ŽŇ◊őÔŌŖĹ‚őŲ ĹŅ…Ķ√£ļ  £¨Ĺ‚Ķ√£ļ
£¨Ĺ‚Ķ√£ļ  ĽÚ
ĽÚ![]() £¨°ŗA£®©Ā2£¨
£¨°ŗA£®©Ā2£¨ ![]() £©£¨B£®1£¨0£©£¨Ļ īūįłő™£ļ
£©£¨B£®1£¨0£©£¨Ļ īūįłő™£ļ ![]() £Ľ£®©Ā2£¨
£Ľ£®©Ā2£¨ ![]() £©£Ľ£®1£¨0£©£Ľ
£©£Ľ£®1£¨0£©£Ľ
£®2£©ĶĪĶ„N‘ŕy÷Š…Ō Ī£¨°ųAMNő™√őŌŽ»żĹ«–ő£¨»ÁÕľ1£¨ĻżA◊ųAD°Õy÷Š”ŕĶ„D£¨‘ÚAD=2£¨‘ŕ![]() ÷–£¨ŃÓy=0Ņ…«ůĶ√x=©Ā3ĽÚx=1£¨°ŗC£®©Ā3£¨0£©£¨«“A£®©Ā2£¨
÷–£¨ŃÓy=0Ņ…«ůĶ√x=©Ā3ĽÚx=1£¨°ŗC£®©Ā3£¨0£©£¨«“A£®©Ā2£¨ ![]() £©£¨°ŗAC=
£©£¨°ŗAC=![]() =
=![]() £¨”…∑≠’ŘĶń–‘÷ Ņ…÷™AN=AC=
£¨”…∑≠’ŘĶń–‘÷ Ņ…÷™AN=AC=![]() £¨‘ŕRt°ųAND÷–£¨”…ĻīĻ…∂®ņŪŅ…Ķ√DN=
£¨‘ŕRt°ųAND÷–£¨”…ĻīĻ…∂®ņŪŅ…Ķ√DN=![]() =
=![]() =3£¨°ŖOD=
=3£¨°ŖOD=![]() £¨°ŗON=
£¨°ŗON=![]() ©Ā3ĽÚON=
©Ā3ĽÚON=![]() +3£¨ĶĪON=
+3£¨ĶĪON=![]() +3 Ī£¨‘ÚMN£ĺOD£ĺCM£¨”ŽMN=CM√¨∂‹£¨≤ĽļŌŐ‚“‚£¨°ŗNĶ„◊ÝĪÍő™£®0£¨
+3 Ī£¨‘ÚMN£ĺOD£ĺCM£¨”ŽMN=CM√¨∂‹£¨≤ĽļŌŐ‚“‚£¨°ŗNĶ„◊ÝĪÍő™£®0£¨ ![]() ©Ā3£©£Ľ
©Ā3£©£Ľ
ĶĪMĶ„‘ŕy÷Š…Ō Ī£¨‘ÚM”ŽO÷ōļŌ£¨ĻżN◊ųNP°Õx÷Š”ŕĶ„P£¨»ÁÕľ2£¨‘ŕRt°ųAMD÷–£¨AD=2£¨OD=![]() £¨°ŗtan°ŌDAM=
£¨°ŗtan°ŌDAM=![]() =
=![]() £¨°ŗ°ŌDAM=60°„£¨°ŖAD°őx÷Š£¨°ŗ°ŌAMC=°ŌDAO=60°„£¨”÷”…’ŘĶĢŅ…÷™°ŌNMA=°ŌAMC=60°„£¨°ŗ°ŌNMP=60°„£¨«“MN=CM=3£¨°ŗMP=
£¨°ŗ°ŌDAM=60°„£¨°ŖAD°őx÷Š£¨°ŗ°ŌAMC=°ŌDAO=60°„£¨”÷”…’ŘĶĢŅ…÷™°ŌNMA=°ŌAMC=60°„£¨°ŗ°ŌNMP=60°„£¨«“MN=CM=3£¨°ŗMP=![]() MN=
MN=![]() £¨NP=
£¨NP=![]() MN=
MN=![]() £¨°ŗīň ĪNĶ„◊ÝĪÍő™£®
£¨°ŗīň ĪNĶ„◊ÝĪÍő™£®![]() £¨
£¨ ![]() £©£Ľ
£©£Ľ
◊Ř…ŌŅ…÷™NĶ„◊ÝĪÍő™£®0£¨ ![]() ©Ā3£©ĽÚ£®
©Ā3£©ĽÚ£®![]() £¨
£¨ ![]() £©£Ľ
£©£Ľ
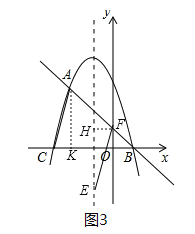
£®3£©ĘŔĶĪACő™∆Ĺ––ňńĪŖ–őĶńĪŖ Ī£¨»ÁÕľ3£¨ĻżF◊ų∂‘≥∆÷ŠĶńīĻŌŖFH£¨ĻżA◊ųAK°Õx÷Š”ŕĶ„K£¨‘Ú”–AC°őEF«“AC=EF£¨°ŗ°ŌACK=°ŌEFH£¨‘ŕ°ųACKļÕ°ųEFH÷–£¨°Ŗ°ŌACK=°ŌEFH£¨°ŌAKC=°ŌEHF£¨AC=EF£¨°ŗ°ųACK°’°ųEFH£®AAS£©£¨°ŗFH=CK=1£¨HE=AK=![]() £¨°ŖŇ◊őÔŌŖ∂‘≥∆÷Šő™x=©Ā1£¨°ŗFĶ„ĶńļŠ◊ÝĪÍő™0ĽÚ©Ā2£¨°ŖĶ„F‘ŕ÷ĪŌŖAB…Ō£¨°ŗĶĪFĶ„ļŠ◊ÝĪÍő™0 Ī£¨‘ÚF£®0£¨
£¨°ŖŇ◊őÔŌŖ∂‘≥∆÷Šő™x=©Ā1£¨°ŗFĶ„ĶńļŠ◊ÝĪÍő™0ĽÚ©Ā2£¨°ŖĶ„F‘ŕ÷ĪŌŖAB…Ō£¨°ŗĶĪFĶ„ļŠ◊ÝĪÍő™0 Ī£¨‘ÚF£®0£¨ ![]() £©£¨īň ĪĶ„E‘ŕ÷ĪŌŖABŌ¬∑Ĺ£¨°ŗEĶĹy÷ŠĶńĺŗņŽő™EH©ĀOF=
£©£¨īň ĪĶ„E‘ŕ÷ĪŌŖABŌ¬∑Ĺ£¨°ŗEĶĹy÷ŠĶńĺŗņŽő™EH©ĀOF=![]() ©Ā
©Ā![]() =
=![]() £¨ľīEĶ„◊›◊ÝĪÍő™©Ā
£¨ľīEĶ„◊›◊ÝĪÍő™©Ā![]() £¨°ŗE£®©Ā1£¨©Ā
£¨°ŗE£®©Ā1£¨©Ā![]() £©£Ľ
£©£Ľ
ĶĪFĶ„ĶńļŠ◊ÝĪÍő™©Ā2 Ī£¨‘ÚF”ŽA÷ōļŌ£¨≤ĽļŌŐ‚“‚£¨…Š»•£Ľ
ĘŕĶĪACő™∆Ĺ––ňńĪŖ–őĶń∂‘Ĺ«ŌŖ Ī£¨°ŖC£®©Ā3£¨0£©£¨«“A£®©Ā2£¨ ![]() £©£¨°ŗŌŖ∂őACĶń÷–Ķ„◊ÝĪÍő™£®©Ā2.5£¨
£©£¨°ŗŌŖ∂őACĶń÷–Ķ„◊ÝĪÍő™£®©Ā2.5£¨ ![]() £©£¨…ŤE£®©Ā1£¨t£©£¨F£®x£¨y£©£¨‘Úx©Ā1=2°Ń£®©Ā2.5£©£¨y+t=
£©£¨…ŤE£®©Ā1£¨t£©£¨F£®x£¨y£©£¨‘Úx©Ā1=2°Ń£®©Ā2.5£©£¨y+t=![]() £¨°ŗx=©Ā4£¨y=
£¨°ŗx=©Ā4£¨y=![]() ©Āt£¨īķ»Ž÷ĪŌŖABĹ‚őŲ ĹŅ…Ķ√
©Āt£¨īķ»Ž÷ĪŌŖABĹ‚őŲ ĹŅ…Ķ√![]() ©Āt=©Ā
©Āt=©Ā![]() °Ń£®©Ā4£©+
°Ń£®©Ā4£©+![]() £¨Ĺ‚Ķ√t=©Ā
£¨Ĺ‚Ķ√t=©Ā![]() £¨°ŗE£®©Ā1£¨©Ā
£¨°ŗE£®©Ā1£¨©Ā![]() £©£¨F£®©Ā4£¨
£©£¨F£®©Ā4£¨ ![]() £©£Ľ
£©£Ľ
◊Ř…ŌŅ…÷™īś‘ŕ¬ķ◊„ŐűľĢĶńĶ„F£¨īň ĪE£®©Ā1£¨©Ā ![]() £©°ĘF£®0£¨
£©°ĘF£®0£¨ ![]() £©ĽÚE£®©Ā1£¨©Ā
£©ĽÚE£®©Ā1£¨©Ā![]() £©°ĘF£®©Ā4£¨
£©°ĘF£®©Ā4£¨ ![]() £©£ģ
£©£ģ


 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥Őō≤ķ◊®¬ŰĶÍŌķ ŘļňŐ“£¨∆šĹÝľŘő™√Ņ«ßŅň40‘™£¨įī√Ņ«ßŅň60‘™≥Ų Ř£¨∆Ĺĺý√ŅŐžŅ… Ř≥Ų100«ßŅň£¨ļůņīĺ≠Ļż –≥°Ķų≤ť∑ĘŌ÷£¨Ķ•ľŘ√ŅĹĶĶÕ2‘™£¨‘Ú∆Ĺĺý√ŅŐžĶńŌķ ŘŅ…‘Ųľ”20«ßŅň£¨»Űł√◊®¬ŰĶÍŌķ Ř’‚÷÷ļňŐ““™ŌŽ∆Ĺĺý√ŅŐžĽŮņŻ2240‘™£¨«ŽĽōīū£ļ
£®1£©√Ņ«ßŅňļňŐ“”¶ĹĶľŘ∂ŗ…Ŕ‘™£Ņ
£®2£©‘ŕ∆Ĺĺý√ŅŐžĽŮņŻ≤ĽĪšĶń«ťŅŲŌ¬£¨ő™ĺ°Ņ…ń‹»√ņŻ”ŕĻňŅÕ£¨”ģĶ√ –≥°£¨ł√ĶÍ”¶įī‘≠ ŘľŘĶńľł’Ř≥Ų Ř£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ≤ĽÕł√ųĶńīŁ◊”÷–”–ňń’ŇĪÍ◊Ň ż◊÷1£¨2£¨3£¨4ĶńŅ®∆¨£¨–°√ų°Ę–°Ľ™ŃĹ»ňįī’’łų◊‘ĶńĻś‘ÚÕś≥ťŅ®∆¨”őŌ∑£ģ–°√ųĽ≠≥Ų ų◊īÕľ»ÁÕľňý ĺ£ļ

–°Ľ™Ń–≥ŲĪŪłŮ»ÁŌ¬£ļ
1 | 2 | 3 | 4 | |
1 | £®1£¨1£© | £®2£¨1£© | £®3£¨1£© | £®4£¨1£© |
2 | £®1£¨2£© | £®2£¨2£© | ĘŔ | £®4£¨2£© |
3 | £®1£¨3£© | £®2£¨3£© | £®3£¨3£© | £®4£¨3£© |
4 | £®1£¨4£© | £®2£¨4£© | £®3£¨4£© | £®4£¨4£© |
£®1£©łýĺ› ų–őÕľ∑÷őŲ£¨–°√ųĶń”őŌ∑Ļś‘Ú «£¨ňśĽķ≥ť≥Ų“Ľ’ŇŅ®∆¨ļů £®ŐÓ°į∑ŇĽō°ĪĽÚ°į≤Ľ∑ŇĽō°Ī£©£¨‘ŔňśĽķ≥ť≥Ų“Ľ’ŇŅ®∆¨£Ľłýĺ›ĪŪłŮ∑÷őŲ£¨–°Ľ™Ķń”őŌ∑Ļś‘Ú «£¨ňśĽķ≥ť≥Ų“Ľ’ŇŅ®∆¨ļů £®ŐÓ°į∑ŇĽō°ĪĽÚ°į≤Ľ∑ŇĽō°Ī£©£¨‘ŔňśĽķ≥ť≥Ų“Ľ’ŇŅ®∆¨°£
£®2£©łýĺ›–°Ľ™Ķń”őŌ∑Ļś‘Ú£¨ĪŪłŮ÷–ĘŔĪŪ ĺĶń”––Ú ż∂‘ő™°° °° °£
£®3£©Ļś∂®ŃĹīő≥ťĶĹĶń ż◊÷÷ģļÕő™∆ś żĶńĽŮ §£¨ň≠ĽŮ §ĶńŅ…ń‹–‘īů£Ņő™ ≤√ī£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ń∂Ń”ŽņŪĹ‚£ļ
Õľ1 «ĪŖ≥§∑÷Īūő™aļÕb£®a£ĺb£©ĶńŃĹłŲĶ»ĪŖ»żĹ«–ő÷Ĺ∆¨ABCļÕC°šDEĶĢ∑Ň‘ŕ“Ľ∆ū£®C”ŽC°š÷ōļŌ£©ĶńÕľ–ő£ģ
≤Ŕ◊ų”Ž÷§√ų£ļ
£®1£©≤Ŕ◊ų£ļĻŐ∂®°ųABC£¨Ĺę°ųC°šDE»∆Ķ„Cįīň≥ Ī’Ž∑ĹŌÚ–ż◊™30°„£¨Ń¨Ĺ”AD£¨BE£¨»ÁÕľ2£Ľ‘ŕÕľ2÷–£¨ŌŖ∂őBE”ŽAD÷ģľšĺŖ”–‘ű—ýĶńīů–°ĻōŌĶ£Ņ÷§√ųń„ĶńĹŠ¬Ř£Ľ
£®2£©≤Ŕ◊ų£ļ»ŰĹęÕľ1÷–Ķń°ųC°šDE£¨»∆Ķ„Cįīň≥ Ī’Ž∑ĹŌÚ»ő“‚–ż◊™“ĽłŲĹ«∂»¶Ń£¨Ń¨Ĺ”AD£¨BE£¨»ÁÕľ3£Ľ‘ŕÕľ3÷–£¨ŌŖ∂őBE”ŽAD÷ģľšĺŖ”–‘ű—ýĶńīů–°ĻōŌĶ£Ņ÷§√ųń„ĶńĹŠ¬Ř£Ľ
≤¬ŌŽ”Ž∑ĘŌ÷£ļ
£®3£©łýĺ›…Ō√śĶń≤Ŕ◊ųĻż≥Ő£¨«Žń„≤¬ŌŽĶĪ¶Ńő™∂ŗ…Ŕ∂» Ī£¨ŌŖ∂őADĶń≥§∂»◊Óīů «∂ŗ…Ŕ£ŅĶĪ¶Ńő™∂ŗ…Ŕ∂» Ī£¨ŌŖ∂őADĶń≥§∂»◊Ó–° «∂ŗ…Ŕ£Ņ
°°
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ∑Ĺ≥Ő£®x©Ā2£©£®x+1£©=x©Ā2ĶńĹ‚ «£® £©
A.x=0
B.x=2
C.x=2ĽÚx=©Ā1
D.x=2ĽÚx=0
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–‘ň∂Į–ő Ĺ Ű”ŕ–ż◊™Ķń «( )
A. ‘ŕŅ’÷–…Ō…żĶń«‚∆Ý«Ú B. ∑…≥ŘĶńĽū≥Ķ
C. Ī÷”…Ō÷”įŕĶńįŕ∂Į D. ‘ň∂Į‘Ī÷ņ≥ŲĶńĪÍ«Ļ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁĻŻ»żĹ«–őĶńŃĹĪŖ≥§∑÷Īūő™3ļÕ5£¨‘Ú÷‹≥§LĶń»°÷Ķ∑∂őß «£® £©
A.6£ľL£ľ15
B.6£ľL£ľ16
C.11£ľL£ľ13
D.10£ľL£ľ16
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°ŅŌ¬Ń–∂‘“Ľ‘™∂Ģīő∑Ĺ≥Őx2+x©Ā3=0łýĶń«ťŅŲĶńŇ–∂Ō£¨’ż»∑Ķń «£®°°°°£©
A. ”–ŃĹłŲ≤ĽŌŗĶ» Ķ żłý B. ”–ŃĹłŲŌŗĶ» Ķ żłý
C. ”–«“÷Ľ”–“ĽłŲ Ķ żłý D. √Ľ”– Ķ żłý
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ∂®“Ś–¬‘ňň„£ļA*B=A+B+AB£¨‘ÚŌ¬Ń–ĹŠ¬Ř’ż»∑Ķń «( £©
ĘŔ2*1=5 Ęŕ2*(-3£©= -7 ĘŘ(-5 £©*8=37 Ę‹(-7£©*(-9£©=47
A. ĘŔĘŕB. ĘŔĘŕĘŘC. ĘŘĘ‹D. ĘŔĘŕĘ‹
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com