
【题目】计算23的结果是 .
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依此类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,2,4,8,…为等比数列,其中a1=1,公比为q=2.
则:
(1)等比数列3,6,12,…的公比q为 , 第6项是 .
(2)如果一个数列a1 , a2 , a3 , a4 , …是等比数列,且公比为q,那么根据定义可得到: ![]() =q,
=q, ![]() =q,
=q, ![]() =q,…
=q,… ![]() =q.
=q.
所以:a2=a1q,a3=a2q=(a1q)q=a1q2 , a4=a3q=(a1q2)q=a1q3 , …
由此可得:an=(用a1和q的代数式表示).
(3)对等比数列1,2,4,…,2n﹣1求和,可采用如下方法进行:
设S=1+2+4+…+2n﹣1 ①,
则2S=2+4+…+2n ②,
②﹣①得:S=2n﹣1
利用上述方法计算:1+3+9+…+3n .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以边长为20cm的正三角形纸板的各顶点为端点,在各边上分别截取4cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿图中 虛线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则它的容积为 cm3.
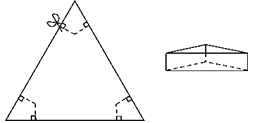
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若( ![]() ☆3)☆(-
☆3)☆(- ![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,( ![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,AF=AB,已知△ABE≌△ADF. 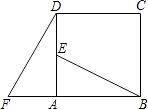
(1)在图中,可以通过平移、翻折、旋转中的哪一种方法,使△ABE变到△ADF的位置;
(2)线段BE与DF有什么关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个运算程序的示意图,若开始输入的x值为81,我们看到第一次输出的结果为27,第二次输出的结果为9,…,第2017次输出的结果为( )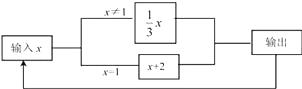
A.1
B.3
C.9
D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角形的直角顶点放在点O处, 一边OM在射线OB上,另一边ON在直线AB的下方.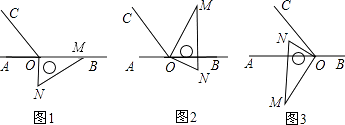
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少秒?(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com