
【题目】已知:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
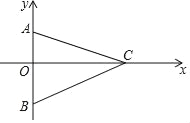
A. △ABC外接圆的圆心在OC上
B. ∠BAC=60°
C. △ABC外接圆的半径等于5
D. OC=12
【答案】D
【解析】
构造含有90°圆心角的⊙P,则⊙P与x轴的交点即为所求的点C.根据△PBA为等腰直角三角形,可得OF=PE=5,根据勾股定理得:CF=7,进而得出OC.
解:
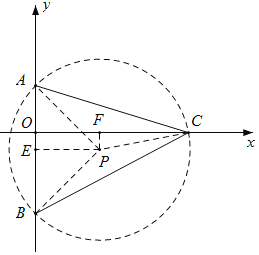
设线段BA的中点为E,
∵点A(0,4),B(0,-6),
∴AB=10,E(0,-1).
如图所示,过点E在第四象限作EP⊥BA,且EP=![]() AB=5,则
AB=5,则
易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5![]() ;
;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=![]() ∠BPA=45°,即则点C即为所求.
∠BPA=45°,即则点C即为所求.
过点P作PF⊥x轴于点F,则OF=PE=5,PF=OE=1,
在Rt△PFC中,PF=1,PC=5![]() ,
,
由勾股定理得:CF=![]() =7,
=7,
∴OC=OF+CF=5+7=12,
故选:D.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
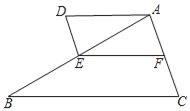
【题目】如图,已知点D在△ABC的外部,AD∥BC,点E在边AB上,ABAD=BCAE.
(1)求证:∠BAC=∠AED;
(2)在边AC取一点F,如果∠AFE=∠D,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
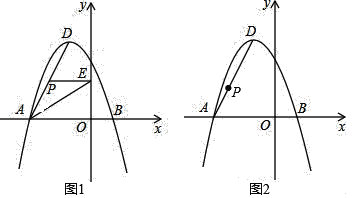
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3经过A(﹣3,0)、B(1,0)两点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合).
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如图1,过点P作PE⊥y轴于点E.求△PAE面积S的最大值;
(3)如图2,抛物线上是否存在一点Q,使得四边形OAPQ为平行四边形?若存在求出Q点坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(1)求证:该抛物线与x轴总有交点;
(2)若该抛物线与x轴有一个交点的横坐标大于3且小于5,求m的取值范围;
(3)设抛物线![]() 与
与![]() 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线![]() 的对称点恰好是点M,求
的对称点恰好是点M,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3的3个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为6,则可获得50元代金券一张;若所得的数字之和为5,则可获得30元代金券一张;若所得的数字之和为4,则可获得15元代金券一张;其它情况都不中奖.
(1)请用列表或树状图的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来.
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
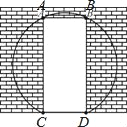
【题目】如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=![]() 米.
米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
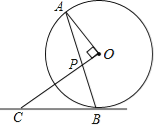
【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为![]() ,OP=1,求BC的长.
,OP=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
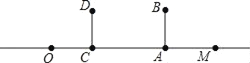
【题目】如图,身高1.6米的小明从距路灯的底部(点O)20米的点A沿AO方向行走14米到点C处,小明在A处,头顶B在路灯投影下形成的影子在M处.
(1)已知灯杆垂直于路面,试标出路灯P的位置和小明在C处,头顶D在路灯投影下形成的影子N的位置.
(2)若路灯(点P)距地面8米,小明从A到C时,身影的长度是变长了还是变短了?变长或变短了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
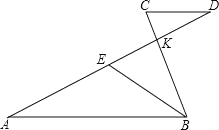
【题目】如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点,
(1)若BK=![]() KC,求
KC,求![]() 的值;
的值;
(2)联结BE,若BE平分∠ABC,则当AE=![]() AD时,猜想线段AB、BC、CD三者之间有怎样的数量关系?请写出你的结论并予以证明;
AD时,猜想线段AB、BC、CD三者之间有怎样的数量关系?请写出你的结论并予以证明;
(3)试探究:当BE平分∠ABC,且AE=![]() AD(n>2)时,线段AB、BC,CD三者之间有怎样的数量关系?请直接写出你的结论,不必证明.
AD(n>2)时,线段AB、BC,CD三者之间有怎样的数量关系?请直接写出你的结论,不必证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com