
����Ŀ��ֱ��y=�� ![]() x+4��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
x+4��x�ύ�ڵ�A����y�ύ�ڵ�B������ABCD��ͼ������ƽ��ֱ������ϵ�У����е�D��x�Ḻ�����ϣ�ֱ��y=x+m������C����x���ڵ�E��
����ֱ��д����C����D�����꣬�����m��ֵ��
�ڵ�P��0��t�����߶�OB�ϵ�һ�����㣨��P����0��B�غϣ���
������P��ƽ����x���ֱ�߽�AB��M����CE��N�����߶�MN�ij���Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д�Ա�����ȡֵ��Χ����
�۵�t=2ʱ���߶�MN��BC��AE֮����ʲô��ϵ����д�����̣�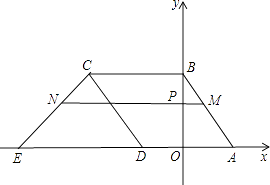
���𰸡��⣺�١�ֱ��y=�� ![]() x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
x+4��x�ύ�ڵ�A����y�ύ�ڵ�B��
���A��������3��0����B��������0��4����
���ı���ABCD�����Σ�
��ֱ��y=x+m������C��
��m=9��
�ڡ�MN ������P��0��t����ƽ����x�ᣬ
������M��������xM �� t������N��������xN �� t����
�ߵ�M��ֱ��AB�ϣ�
ֱ��AB�Ľ���ʽΪy=�� ![]() x+4��
x+4��
��t=�� ![]() xM+4����xM=��
xM+4����xM=�� ![]() t+3��
t+3��
ͬ����N��ֱ��CE�ϣ�ֱ��CE�Ľ���ʽΪy=x+9��
��t=xN+9����xN=t��9��
��MN��x�����߶�MN�ij���Ϊd��
��d=xM��xN=�� ![]() t+3����t��9��=��
t+3����t��9��=�� ![]() t+12��0��t��4��
t+12��0��t��4��
��MN= ![]() ��BC+AE����
��BC+AE����
���ɣ���t=2ʱ��P��0��2����
��OP=2��
��OB=4��
���P��OB�е㣬
��MN��x�ᣬ
��MN������ABCE����λ�ߣ�
��MN= ![]() ��BC+AE����
��BC+AE����
������������ֱ�ߵĽ���ʽ�����A��B������꣬�ٸ������ε����ʼ��������C����D�����꣬�ѵ�C���������ֱ��y=x+m�������m��ֵ�������M������Ϊ��xM �� t������N������Ϊ��xN �� t�����������xM=�� ![]() t+3�������xN=t��9�������õ�d=xM��xN=��
t+3�������xN=t��9�������õ�d=xM��xN=�� ![]() t+3����t��9��=��
t+3����t��9��=�� ![]() t+12�����������P�����꣬�����ó���P��OB�е㣬���ɵó�MN������ABCE����λ���ɵó����ۣ�
t+12�����������P�����꣬�����ó���P��OB�е㣬���ɵó�MN������ABCE����λ���ɵó����ۣ�


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳������ס���������Ʒ�����м�����Ʒ����Ϊ120Ԫ/�����ۼ�Ϊ130Ԫ/����������Ʒ����Ϊ100Ԫ/�����ۼ�Ϊ150Ԫ/����
��1�����̳���36000Ԫ������������Ʒ���ɣ��������ɻ�����6000Ԫ������̳������ס���������Ʒ�����ټ������з�������
��2�����̳�������������Ʒ��100�����蹺��������Ʒx����������Ʒ���ۺ�ɻ�������ΪyԪ����д��y��x�ĺ�����ϵʽ����Ҫ��д���Ա���x�ķ�Χ������ָ������������Ʒ����x������ʱ��������y�����ӻ��Ǽ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0��ͼ���ϲ��ֵ�����꣨x��y����Ӧֵ�б����£�
x | �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
y | �� | ��3 | ��2 | ��3 | ��6 | ��11 | �� |
��ú���ͼ��ĶԳ����ǣ� ��
A.ֱ��x=��3
B.ֱ��x=��2
C.ֱ��x=��1
D.ֱ��x=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABO�У���OAB=90�㣬��AOB=30�㣬OB=8����OBΪһ�ߣ��ڡ�OAB�����ȱ�������OBC��D��OB���е㣬����AD���ӳ���OC��E��
��1�����B�����ꣻ
��2����֤���ı���ABCE��ƽ���ı��Σ�
��3����ͼ2����ͼ1�е��ı���ABCO�۵���ʹ��C���A�غϣ��ۺ�ΪFG����OG�ij���
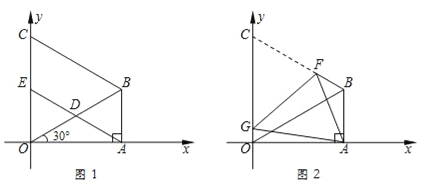
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1��![]() +|1��
+|1�� ![]() |+��
|+�� ![]() ����1��20170
����1��20170
��2��![]() ��
�� ![]() ����
���� ![]() ��1��2 ��
��1��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.��5�ǩ�25��ƽ����
B.3�ǣ���3��2������ƽ����
C.����2��2��ƽ������2
D.8��ƽ�����ǡ�4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ҡ�������վ��ѧУ��һ����ֱ�Ĺ�·�ԣ�С���ҡ�ѧУ��������·�ľ�����Բ��ƣ���һ�죬С���Ӽҳ���ȥ��ѧ����������·���е�������վǡ�ó���һ������������������������·������ʻ��С���³�ʱ���ֻ���4�����ϿΣ���������������·�ܲ��ϵ�ѧУ���ϡ��³�ʱ����Բ��ƣ���С����ҵľ���s����λ���ף���������ʱ��t����λ�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ����֪С���Ӽҳ���7����ʱ��ҵľ���Ϊ1200�ף����Ϲ�������������ѧУ����10���ӣ�����˵����
��С���Ӽҳ���5����ʱ���Ϲ����� �ڹ��������ٶ�Ϊ400��/����
��С���¹�����������ѧУ���ٶ�Ϊ100��/���� ��С���Ͽ�û�гٵ�
������ȷ�ĸ����ǣ� ��
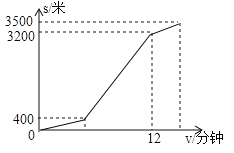
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com