
【题目】请将下面证明中每一步的理由填在括号内.
已知:如图,D,E,F分别是BC,CA,AB上的点,DE∥BA,DF∥CA.
求证:∠FDE=∠A
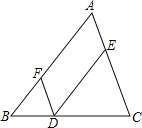
证明:∵ DE∥BA( )
∴∠FDE=∠BFD( )
∵DF∥CA( )
∴∠BFD=∠A( )
∴∠FDE=∠A( )
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
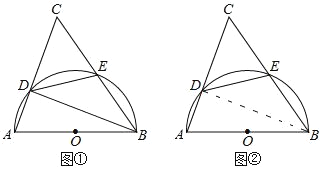
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市拟将徽州大道南延至庐江县庐城镇,庐江段的一段土方工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该土方工程分成两部分,甲队做完其中一部分工程用了x天,乙队做完另一部分工程用了y天,若x,y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,请用含x的式子表示y,并求出两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF.已知AB = 4cm,AD = 2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
(说明:补全表格时相关数值保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(4)结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
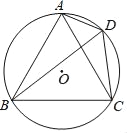
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.
(1)如图1,若O为AB的中点,以O为圆心,OB为半径作⊙O交BC于点D,过D作DE⊥AC,垂足为E.
①试说明:BD=CD;
②判断直线DE与⊙O的位置关系,并说明理由.
(2)如图2,若点O沿OB向点B移动,以O为圆心,以OB为半径作⊙O与AC相切于点F,与AB相交于点G,与BC相交于点D,DE⊥AC,垂足为E,已知⊙O的半径长为4,CE=2,求切线AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com