Question

20．如图，已知AB∥CD，直线l分别截AB、CD于E、C两点，M是线段EC上一动点（不与E、C重合），过M点作MN⊥CD于点N，连结EN．

（1）如图1，当∠ECD=40°时，填空：∠FEB=40°；∠MEN+∠MNE=50°；
（2）如图2，当∠ECD=α°时，猜想∠MEN+∠MNE的度数与α的关系，并证明你的结论．

Answer 1

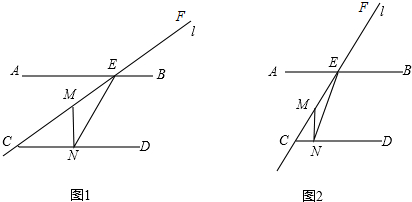
分析 （1）直接根据平行线的性质可得出∠FEB的度数，再由MN⊥CD，由三角形内角和定理可求出∠CMN的度数，根据三角形外角的性质即可得出结论；
（2）根据AB∥CD，∠ECD=α°可得出∠AEC=∠ECD=α°且∠AEN+∠CNE=180°，由MN⊥CD得出∠MNC=90°，根据三角形内角和定理即可得出结论．

解答 解：（1）∵AB∥CD，∠ECD=40°，
∴∠FEB=∠ECD=40°；
∵MN⊥CD，
∴∠CNM=90°，
∴∠CMN=90°-∠ECN=90°-40°=50°．
∵∠CMN是△EMN的外角，
∴∠CMN=∠MEN+∠MNE=50°．
故答案为：40°，50°； 

（2）猜想：∠MEN+∠MNE=90°-α°．
证明如下：∵AB∥CD，∠ECD=α°
∴∠AEC=∠ECD=α°且∠AEN+∠CNE=180°．
又∵MN⊥CD
∴∠MNC=90°，
∴90°+∠MEN+∠MNE+α°=180°，
∴∠MNE+∠MEN=90°-α°．

点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．