
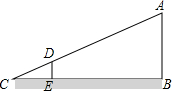
 如图,小亮欲测量一电线杆AB的高度,他站在该电线杆的影子上前后移动,直到他身体影子的顶端正好与电线杆影子的顶端重叠,此时同伴测出小亮与电线杆的距离BE=12m,小亮的影子长CE=4m,已知小亮的身高DE=1.7m.
如图,小亮欲测量一电线杆AB的高度,他站在该电线杆的影子上前后移动,直到他身体影子的顶端正好与电线杆影子的顶端重叠,此时同伴测出小亮与电线杆的距离BE=12m,小亮的影子长CE=4m,已知小亮的身高DE=1.7m.分析 (1)利用平行于三角形一边的直线与其它两边所截得的三角形与原三角形相似可判断△CDE和△CAB相似;
(2)根据三角形相似的性质得$\frac{DE}{AB}$=$\frac{CE}{CB}$,即$\frac{1.7}{AB}$=$\frac{4}{4+12}$,然后利用比例性质求AB即可.
解答 解:(1)△CDE和△CAB相似.理由如下:
∵DE∥AB,
∴△CDE∽△CAB;
(2)∵△CDE∽△CAB,
∴$\frac{DE}{AB}$=$\frac{CE}{CB}$,即$\frac{1.7}{AB}$=$\frac{4}{4+12}$,
∴AB=6.8(m).
答:电线杆AB的高度为6.8m.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
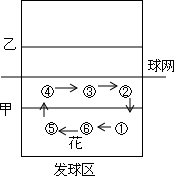 排球比赛中,甲、乙两方上场的各6名队员面对排球网,分别站在排球场的一边,6名队员一般站成两排,从排球场右下角开始,分别为1号位、2号位、3号位、4号位、5号位、6号位.
排球比赛中,甲、乙两方上场的各6名队员面对排球网,分别站在排球场的一边,6名队员一般站成两排,从排球场右下角开始,分别为1号位、2号位、3号位、4号位、5号位、6号位.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
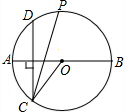 如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )
如图,AB为⊙O的直径,作弦CD⊥AB,∠OCD的平分线交⊙O于点P,当点C在下半圆上移动时,(不与点A、B重合),下列关于点P描述正确的是( )| A. | 到CD的距离保持不变 | B. | 到D点距离保持不变 | ||
| C. | 等分$\widehat{BD}$ | D. | 位置不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com