
【题目】“耕深·志远”是我们浣江初中的核心文化,一个不透明的口袋里装有分别标有汉字“耕”、“深”、“志”、“远”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“耕”的概率为多少.
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“耕深”或“志远”的概率P1.
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“耕深”或“志远”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明)
【答案】![]()
【解析】
(1)汉字“耕”、“深”、“志”、“远”的四个小球,任取一球共有4种结果,即可求出从中任取一个球,球上的汉字刚好是“耕”的概率;
(2)列表得出所有等可能的情况数,找出甲取出的两个球上的汉字恰能组成“耕深”或“志远”的情况即可求出概率P1;
(3)列表得出所有等可能的情况数,找出甲取出的两个球上的汉字恰能组成“耕深”或“志远”的情况即可求出概率P2.
(1)∵有汉字“耕”、“深”、“志”、“远”的四个小球,任取一球,共有4种不同结果,
∴球上汉字是“鄞”的概率为P=![]() ;
;
(2)列表如下:
耕 | 深 | 志 | 远 | |
耕 | --- | (深,耕) | (志,耕) | (远,耕) |
深 | (耕,深) | --- | (志,深) | (远,深) |
志 | (耕,志) | (深,志) | --- | (远,志) |
远 | (耕,远) | (深,远) | (志,远) | --- |
所有等可能的情况有12种,其中取出的两个球上的汉字恰能组成“耕深”或“志远”的情况有4种,
则P1=![]() ;
;
(3)列表如下:
耕 | 深 | 志 | 远 | ||
耕 | (耕,耕) | (深,耕) | (志,耕) | (远,耕) | |
深 | (耕,深) | (深,深) | (志,深) | (远,深) | |
志 | (耕,志) | (深,志) | (志,志) | (远,志) | |
远 | (耕,远) | (深,远) | (志,远) | (远,远) |
所有等可能的情况有16种,其中取出的两个球上的汉字恰能组成“美丽”或“鄞州”的情况有4种,
则P2=![]() ,P1>P2.
,P1>P2.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
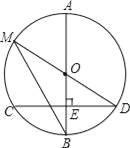
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
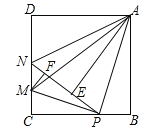
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数
的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数![]() 的图象上,则下列结论正确的是( )
的图象上,则下列结论正确的是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
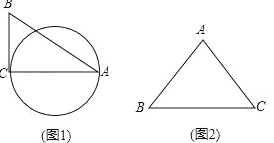
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“友好圆”.
(1)如图1,△ABC中,∠C=90°,AB=13,BC=5,则AC边上的友好圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=10,BC=12,画草图并求出它所有的友好圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,其中
两点,其中![]() 点坐标为
点坐标为![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
(3)一次函数的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数图象上的一个动点,若
是反比例函数图象上的一个动点,若![]() ,求此时
,求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com