
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“友好圆”.
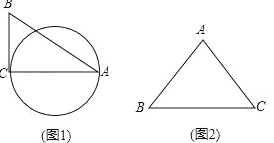
(1)如图1,△ABC中,∠C=90°,AB=13,BC=5,则AC边上的友好圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=10,BC=12,画草图并求出它所有的友好圆的半径.
【答案】⑴6 ;⑵![]()
【解析】
(1)先依据勾股定理求得AC的长,然后依据切线的性质可知AC为圆的直径,故此可求得△BAC的友好圆的半径等于AC的一半;
(2)当O在BC上时,连接OD,过点A作AE⊥BC.由等腰三角形的性质和勾股定理求得AE=8,依据切线的性质可证明OD⊥AB,接下来证明△ODB∽△AEB,由相似三角形的性质可求得圆O的半径;当O在AB上且圆O与BC相切时,连接OD、过点A作AE⊥BC,垂足为E.先证明△BOD∽△BAE,由相似三角形的性质可求得圆O的半径,当O在AB上且圆O与AC相切时,连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.先依据面积法求得BF的长,然后再证明△AOD∽△ABF,由相似三角形的性质可求得圆O的半径;
(1)∵∠C=90°,AB=13,BC=5,
∴AC=![]() .
.
∵BC是圆的切线,∠BCA=90°,
∴AC为圆的直径.
∴AC边上的半随圆的半径为6.
(2)当O在BC上时,如图(1)所示:连接OD,过点A作AE⊥BC.
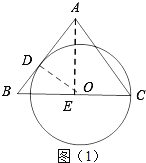
∵AB=AC,AE⊥BC,
∴BE=EC=6.
在△AEB中,由勾股定理可知AE=![]() =8.
=8.
∵AB与⊙O相切,
∴OD⊥AB.
∴∠BDO=∠BEA=90°.
又∵∠OBD=∠EBA,
∴△ODB∽△AEB.
∴![]() .
.
设⊙O的半径为r.在OB=12-r.
∴![]() .
.
∴r=![]() .
.
∴△ABC的BC边上的友好圆的半径为![]() .
.
当O在AB上时,如图(2),连接OD、过点A作AE⊥BC,垂足为E.
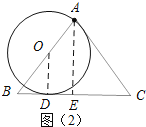
∵BC与⊙O相切,
∴OD⊥BC.
又∵AE⊥BC,
∴OD∥AE.
∴△BOD∽△BAE.
∴![]() .
.
设⊙O的半径为r,则OB=10-r.
∴![]() .
.
∴r=![]() .
.
如图(3)所示:连接OD、过点B作BF⊥AC,过点A作AE⊥BC,垂足为E.
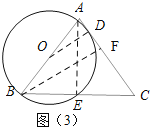
∵S△ABC=![]() BCAE=
BCAE=![]() ACBF,
ACBF,
∴![]() ×12×8=
×12×8=![]() ×10×BF.
×10×BF.
∴BF=9.6.
∵AC与⊙O相切,
∴DO⊥AC.
∴DO∥BF.
∴△AOD∽△ABF.
∴![]()
即![]() .
.
∴r=![]() .
.
综上所述,△ABC的友好圆的半径分为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
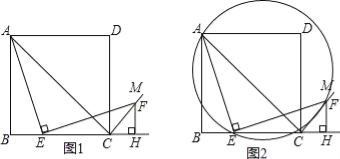
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂决定把一块长100m、宽60m的矩形空地建成停车场.设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为停车位,且四周的4个出口宽度相同,其宽度不小于28m,不大于52m.设绿化区较长边为xm,停车场的面积为ym2
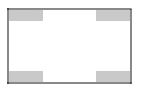
(1)直接写出:
①用x的式子表示出口的宽度为_____.
②y与x的函数关系式及x的取值范围.
(2)求停车场的面积y的最大值.
(3)预计停车场造价为100元/m2,绿化区造价为50元/m2.如果汽车厂投资不得超过540000元建造,当x为整数时,共有几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
我们已经学习了一元二次方程的多种解法:如因式分解法,开平方法,配方法和公式法,还可以运用十字相乘法,请从以下一元二次方程中任选两个,并选择你认为适当的方法解这个方程.
①![]() ②
②![]() ③
③![]() ④
④![]()
我选择第 个方程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“耕深·志远”是我们浣江初中的核心文化,一个不透明的口袋里装有分别标有汉字“耕”、“深”、“志”、“远”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“耕”的概率为多少.
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“耕深”或“志远”的概率P1.
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“耕深”或“志远”的概率为P2,指出P1,P2的大小关系(请直接写出结论,不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
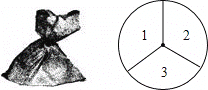
【题目】一个不透明的袋子中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由转动的转盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小亮和小丽想通过游戏来决定谁代表学校参加歌咏比赛.游戏规则为:一人从袋子中摸出一个小球,另一个人转动转盘,如果从袋中所摸球上的数字与转盘上转出数字之和小于4,那么小丽去,否则小亮去.
(1)请用适当的方法求小丽参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
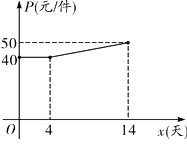
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com