
【题目】某汽车厂决定把一块长100m、宽60m的矩形空地建成停车场.设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为停车位,且四周的4个出口宽度相同,其宽度不小于28m,不大于52m.设绿化区较长边为xm,停车场的面积为ym2
(1)直接写出:
①用x的式子表示出口的宽度为_____.
②y与x的函数关系式及x的取值范围.
(2)求停车场的面积y的最大值.
(3)预计停车场造价为100元/m2,绿化区造价为50元/m2.如果汽车厂投资不得超过540000元建造,当x为整数时,共有几种建造方案?
【答案】(1)①(100﹣2x)m;②y=﹣4x2+80x+6000(24≤x≤36);(2)5616m2;(3)共有3种建造方案.
【解析】
(1)①根据图形可得结论;②根据题意可得y与x的关系式;
(2)根据二次函数的增减性可得结论;
(3)根据列方程即可得到结论.
解:(1)①出口的宽度为:100﹣2x,
②根据题意得,y=100×60﹣4x(x﹣20),
即y与x的函数关系式及x的取值范围为:y=﹣4x2+80x+6000(24≤x≤36);
故答案为:(100﹣2x)m;
(2)y=﹣4x2+80x+6000=﹣4(x﹣10)2+6400,
∵a=﹣4<0,抛物线的开口向下,对称轴为x=10,当24≤x≤36时,y随x的增大而减小,
∴当x=24时,y最大=5616,
答:停车场的面积y的最大面积为5616m2;
(3)设费用为w,
由题意得,w=100(﹣4x2+80x+6400)+50×4x(x﹣20)=﹣200(x﹣10)2+660000,
∴当w=540000时,解得:x1=﹣10![]() +10,x2=10
+10,x2=10![]() +10,
+10,
∵a=﹣100<0,
∴x1=﹣10![]() +10,x2=10
+10,x2=10![]() +10,w=540000,
+10,w=540000,
∵24≤x≤36,
∴10![]() +10≤x≤36,且x为整数,
+10≤x≤36,且x为整数,
∴共有3种建造方案.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】已知x1、x2是方程x2﹣(k﹣2)x+k2+3k+5=0的两个实数根,则x12+x22的最大值是( )
A. 19 B. 18 C. 15 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
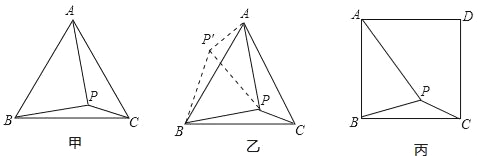
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,若双曲线![]() (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线![]() (k>0)的对径.
(k>0)的对径.

(1)求双曲线![]() 的对径;
的对径;
(2)若某双曲线![]() (k>0)的对径是
(k>0)的对径是![]() .求k的值.
.求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x+2交x轴、y轴分别于点A、B,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣![]() ,且抛物线经过A、B两点,交x轴于另一点C.
,且抛物线经过A、B两点,交x轴于另一点C.
(1)求抛物线的解析式;
(2)点M是抛物线x轴上方一点,∠MBA=∠CBO,求点M的坐标;
(3)过点A作AB的垂线交y轴于点D,平移直线AD交抛物线于点E、F两点,连结EO、FO.若△EFO为以EF为斜边的直角三角形,求平移后的直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
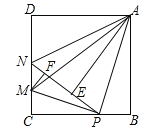
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:圆心在三角形的一边上,与另一边相切,且经过三角形一个顶点(非切点)的圆,称为这个三角形圆心所在边上的“友好圆”.
(1)如图1,△ABC中,∠C=90°,AB=13,BC=5,则AC边上的友好圆的半径为 .
(2)如图2,已知等腰△ABC,AB=AC=10,BC=12,画草图并求出它所有的友好圆的半径.
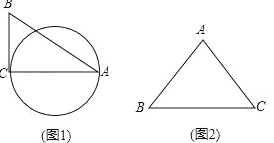
查看答案和解析>>
科目:初中数学 来源: 题型:
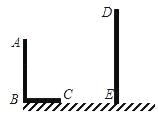
【题目】如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m,同时测量出DE在阳光下的投影长为6m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)请你计算DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com