
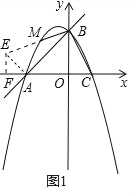
����Ŀ����ͼ����ֱ֪��y��x+2��x�ᡢy��ֱ��ڵ�A��B��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x����![]() ���������߾���A��B���㣬��x������һ��C��
���������߾���A��B���㣬��x������һ��C��
��1���������ߵĽ���ʽ��
��2����M��������x���Ϸ�һ�㣬��MBA����CBO�����M�����ꣻ
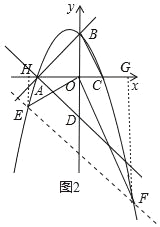
��3������A��AB�Ĵ��߽�y���ڵ�D��ƽ��ֱ��AD���������ڵ�E��F���㣬����EO��FO������EFOΪ��EFΪб�ߵ�ֱ�������Σ���ƽ�ƺ��ֱ�ߵĽ���ʽ��

���𰸡���1��y����x2��x+2����2��M����![]() ��
��![]() ������3��ƽ�ƺ�Ľ���ʽΪy����x��1+
������3��ƽ�ƺ�Ľ���ʽΪy����x��1+![]() ��y����x��1��
��y����x��1��![]() ��
��
��������
��1�����ô���ϵ�������ɽ�����⣻
��2����ͼ1�У���EA��AB��BM���ӳ�����E����EF��x����F�������E���꣬�����ֱ��BE�Ľ���ʽ�����÷����鼴�ɽ�����⣻
��3����ͼ2�У���ֱ��AD����ƽ��ʱ����E��x1��y1����F��x2��y2������EH��x����H��FG��x����G���������������ε������Լ�����ϵ����ϵ���������鼴�ɽ�����⣻
��1����ֱ��y��x+2��x�ᡢy��ֱ��ڵ�A��B��
��A����2��0����B��0��2����
�������ߵĶԳ���x����![]() ��A��C���ڶԳ���Գƣ�
��A��C���ڶԳ���Գƣ�
��C��1��0����
�������ߵĽ���ʽΪy��a��x+2����x��1�����ѣ�0��2������õ�a����1��
�������ߵĽ���ʽΪy����x2��x+2��
��2����ͼ1�У���EA��AB��BM���ӳ�����E����EF��x����F��
�ߡ�ABE����OBC����BAE����BOC��90�㣬
���BAE�ס�BOC��
��![]() ��
��
��![]() ��
��
��AE��![]() ��
��
�ߡ�EAF+��BAO��90�㣬��BAO��45�㣬
���EAF��45�㣬
��EF��AF��1��
��E��3��1����
��ֱ��BE�Ľ���ʽΪy����![]() x+2��
x+2��
��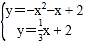 �����
�����![]() ��
��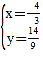 ��
��
��M��-![]() ��
��![]() ����
����
��3����ͼ2�У���ֱ��AD����ƽ��ʱ����E��x1��y1����F��x2��y2������EH��x����H��FG��x����G��
�ߡ�EOF=90��=��PHE=��OGF��
����EHO�ס�OGF�õ���
![]() ��
��
��![]() ��
��
��x1x2+y1y2=0��
��![]() ����ȥy�õ���x2+b-2=0��
����ȥy�õ���x2+b-2=0��
��x1x2=b-2��x1+x2=0��y1y2=��-x1+b����-x2+b��=x1x2+b2��
��2��b-2��+b2=0��
���b=-1-![]() ��-1+
��-1+![]() ����������
����������
��ֱ��AD����ƽ��ʱ��ͬ���ɵ�b=-1+![]() ��
��
����������ƽ�ƺ�Ľ���ʽΪy=-x-1+![]() ��y=-x-1-
��y=-x-1-![]() ��
��


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д� Ӧ����㲦ϵ�д�
Ӧ����㲦ϵ�д� ״Ԫ����ϵ�д�
״Ԫ����ϵ�д� ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��ͼ���㣨4��3������3��0����
��1����b��c��ֵ��
��2������ö��κ���ͼ��Ķ�������ͶԳ��ᣬ������������ϵ�л����ú�����ͼ����
��3���ú�����ͼ��������ƽ�Ƶõ�y=x2��ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
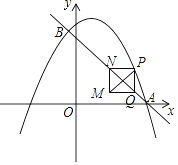
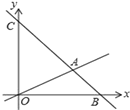
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��x+3��������![]() ����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ
����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ![]() ������P�����������˶��������A��B�غϣ�������P��y���ƽ���ߣ���ֱ��AB�ڵ�Q����PQ����y���غ�ʱ����PQΪ����������PQMN��ʹMN��y����PQ��ͬ�࣬����PM�����P�ĺ�����Ϊm��
������P�����������˶��������A��B�غϣ�������P��y���ƽ���ߣ���ֱ��AB�ڵ�Q����PQ����y���غ�ʱ����PQΪ����������PQMN��ʹMN��y����PQ��ͬ�࣬����PM�����P�ĺ�����Ϊm��
��1����b��c��ֵ��
��2������N����ֱ��AB��ʱ��ֱ��д��m��ȡֵ��Χ��
��3������P��A��B����֮������������˶�ʱ����������PQMN���ܳ�ΪC����C��m֮��ĺ�����ϵʽ����д��C��m���������ʱm��ȡֵ��Χ��
��4������PQM����������2��������ʱ��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y��ax2+2��x���ڵ�A����2��0����B����y���ڵ�C��
��1���������ߵĽ���ʽ��
��2����P�ӵ�A��������1����λ/����ٶ����յ�B�˶���ͬʱ��Q�ӵ�C����������ͬ���ٶ���y�������������˶����˶���ʱ��Ϊt�룬����P�����Bʱ����QҲֹͣ�˶�������PQC�����ΪS����S��t��ĺ�����ϵʽ��ֱ��д��t��ȡֵ��Χ��
��3������2���������£�����P���߶�OB��ʱ����PQ��ֱ��AC�ڵ�G����P��PE��AC�ڵ�E����EG�ij���
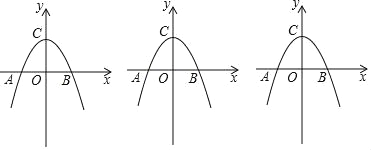
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������һ�鳤100m����60m�ľ��οյؽ���ͣ��������Ʒ�����ͼ��ʾ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊȫ�ȵľ��Σ����հ�����Ϊͣ��λ�������ܵ�4�����ڿ�����ͬ������Ȳ�С��28m��������52m�����̻����ϳ���Ϊxm��ͣ���������Ϊym2
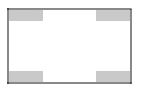
��1��ֱ��д����
����x��ʽ�ӱ�ʾ���ڵĿ���Ϊ_____��
��y��x�ĺ�����ϵʽ��x��ȡֵ��Χ��
��2����ͣ���������y�����ֵ��
��3��Ԥ��ͣ�������Ϊ100Ԫ/m2���̻������Ϊ50Ԫ/m2�����������Ͷ�ʲ��ó���540000Ԫ���죬��xΪ����ʱ�����м��ֽ��췽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����B��6��0����ֱ��AB��ֱ��OA�ཻ�ڵ�A��4��2��������M���߶�OA������AC���˶���
��1����ֱ��AB�Ľ���ʽ��
��2�����OAC�������
��3���Ƿ���ڵ�M��ʹ��OMC������ǡ�OAC�������![]() �������������ʱ��M�����ꣻ�������ڣ�˵�����ɣ�
�������������ʱ��M�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ�̣�
�����Ѿ�ѧϰ��һԪ���η��̵Ķ��ֽⷨ������ʽ�ֽⷨ����ƽ�������䷽����ʽ��������������ʮ����˷����������һԪ���η�������ѡ��������ѡ������Ϊ�ʵ��ķ�����������̣�
��![]() ��
��![]() ��
��![]() ��
��![]()
��ѡ��� �����̡�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
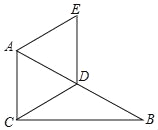
����Ŀ����ͼ����֪Rt��ABC�У���ACB��90�㣬��B��30�㣬D��AB���е㣬AE��CD��AC��ED��
��֤���ı���ACDE�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼijũ��Ҫ��һ�������ε���������������һ�߿�ǽ��ǽ��18m������������ľ��Χ�ɣ�ľ����35m������������ܴﵽ150m2������ܣ����������Ʒ�����������ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com