
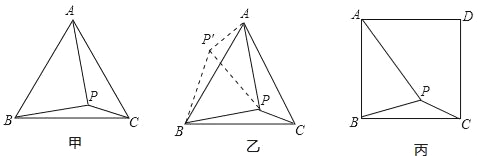
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
【答案】(1)等边 直角 150°;(2)![]() ;(3)135°;(4)
;(3)135°;(4)![]() .
.
【解析】
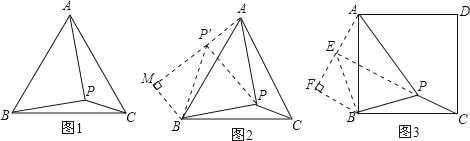
(1)将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠AP′B=150°,而∠BPC=∠AP′B=150°,
(2)过点B作BM⊥AP′,交AP′的延长线于点M,进而求出等边△ABC的边长为![]() ,问题得到解决.
,问题得到解决.
(3)求出![]() ,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
,根据勾股定理的逆定理求出∠AP′P=90°,推出∠BPC=∠AEB=90°+45°=135°;
(4)过点B作BF⊥AE,交AE的延长线于点F,求出FE=BF=1,AF=2,关键勾股定理即可求出AB.
解:(1)∵△ABC是等边三角形,
∴∠ABC=60°,
将△BPC绕点B顺时针旋转60°得出△ABP′,
∴![]()
∵∠PBC+∠ABP=∠ABC=60°,
∴∠ABP′+∠ABP=∠ABC=60°,
∴△BPP′是等边三角形,
∴![]()
∵AP′=1,AP=2,
∴AP′2+PP′2=AP2,
∴∠AP′P=90°,则△PP′A是 直角三角形;
∴∠BPC=∠AP′B=90°+60°=150°;
(2)过点B作BM⊥AP′,交AP′的延长线于点M,
∴![]()
由勾股定理得: ![]()
∴![]()
由勾股定理得: ![]()
故答案为:(1)等边;直角;150;![]() ;
;
(3)将△BPC绕点B逆时针旋转90°得到△AEB,
与(1)类似:可得:AE=PC=1,BE=BP=![]() ,∠BPC=∠AEB,∠ABE=∠PBC,
,∠BPC=∠AEB,∠ABE=∠PBC,
∴∠EBP=∠EBA+∠ABP=∠ABC=90°,
∴![]() ,
,
由勾股定理得:EP=2,
∵![]()
∴AE2+PE2=AP2,
∴∠AEP=90°,
∴∠BPC=∠AEB=90°+45°=135°;
(4)过点B作BF⊥AE,交AE的延长线于点F;
∴∠FEB=45°,
∴FE=BF=1,
∴AF=2;
∴在Rt△ABF中,由勾股定理,得AB=![]() ;
;
∴∠BPC=135°,正方形边长为![]() .
.
答:(3)∠BPC的度数是135°;
(4)正方形ABCD的边长是![]() .
.


科目:初中数学 来源: 题型:
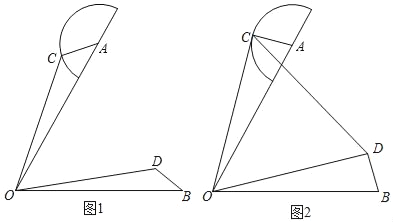
【题目】已知OA=OB=4,∠AOB=60°,半⊙A的半径为1,点C是半圆上任意一点,连结OC,把OC绕点O顺时针旋转6
0°到OD的位置,连结BD.
(1)如图1,求证:AC=BD.
(2)如图2,当OC与半圆相切于点C时,求CD的长.
(3)直接写出△AOC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
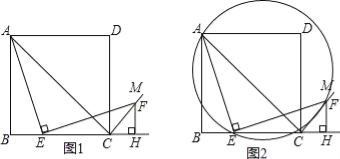
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
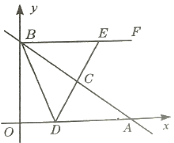
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 点重合),射线
点重合),射线![]() 轴,延长
轴,延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,记
,记![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)是否存在![]() 的值,使得
的值,使得![]() 是以
是以![]() 为腰的等腰三角形?若存在,求出所有符合条件的
为腰的等腰三角形?若存在,求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
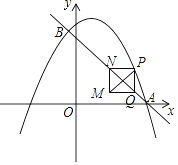
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(3,0),点P在反比例函数y= ![]() 的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
A. 2个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
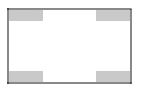
【题目】某汽车厂决定把一块长100m、宽60m的矩形空地建成停车场.设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为停车位,且四周的4个出口宽度相同,其宽度不小于28m,不大于52m.设绿化区较长边为xm,停车场的面积为ym2
(1)直接写出:
①用x的式子表示出口的宽度为_____.
②y与x的函数关系式及x的取值范围.
(2)求停车场的面积y的最大值.
(3)预计停车场造价为100元/m2,绿化区造价为50元/m2.如果汽车厂投资不得超过540000元建造,当x为整数时,共有几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
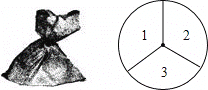
【题目】一个不透明的袋子中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由转动的转盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小亮和小丽想通过游戏来决定谁代表学校参加歌咏比赛.游戏规则为:一人从袋子中摸出一个小球,另一个人转动转盘,如果从袋中所摸球上的数字与转盘上转出数字之和小于4,那么小丽去,否则小亮去.
(1)请用适当的方法求小丽参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com