
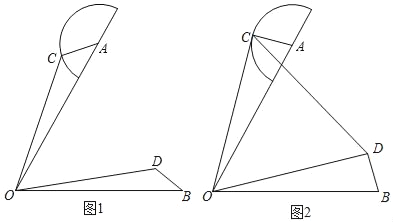
【题目】已知OA=OB=4,∠AOB=60°,半⊙A的半径为1,点C是半圆上任意一点,连结OC,把OC绕点O顺时针旋转6
0°到OD的位置,连结BD.
(1)如图1,求证:AC=BD.
(2)如图2,当OC与半圆相切于点C时,求CD的长.
(3)直接写出△AOC面积的最大值.
【答案】(1)详见解析;(2)![]() ;(3)2.
;(3)2.
【解析】
(1)根据已知条件易证△OAC≌△DOB,由全等三角形的性质即可得AC=BD;(2)根据勾股定理求得OC的长,再证明△COD是等边三角形,根据等边三角形的性质即可得CD的长;(3)当h最大时,S△AOC最大,即当C在半圆A的中点时,h最大,此时h=1,计算面积可得结论.
证明:(1)∵∠AOB=∠COD=60°
∴∠COA+∠AOD=∠BOD+∠AOD
∴∠COA=∠BOD
在△OAC和△OBD中,
∵
∴△OAC≌△DOB(SAS)
∴AC=BD;
(2)如图2,∵OC是⊙A的切线,
∴AC⊥OC,∠OCA=90°,
在Rt△OCA中,由勾股定理得:OC2+AC2=OA2,
∴OC2+12=42,
∴OC=![]() ,
,
在△COD中,∵OC=OD,∠COD=60°,
∴△COD是等边三角形,
∴CD=OC=![]() ;
;
(3)设点C到OA的距离为h,
∵S△AOC=![]() OAh,
OAh,
∵OA=4,
∴当h最大时,S△AOC最大,即当C在半圆A的中点时,h最大,此时h=1,
∴S△AOC=![]() OAh=
OAh=![]() =2.
=2.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从
从![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度运动,点
的速度运动,点![]() 从
从![]() 开始沿
开始沿![]() 边以
边以![]() 的速度移动,如果点
的速度移动,如果点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当其中一点到达
同时出发,当其中一点到达![]() 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为![]() ,当
,当![]() ________时,四边形
________时,四边形![]() 也为矩形.
也为矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
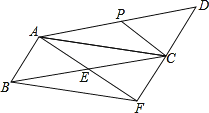
【题目】如图,在平行四边形![]() 中,
中,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,P是AD的中点.
,P是AD的中点.
(1)求证:四边形ABFC是平行四边形;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形AECP是菱形,并说明理由.
满足什么数量关系时,四边形AECP是菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°.
(1)作出经过点B,圆心O在斜边AB上且与边AC相切于点E的⊙O(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)设(1)中所作的⊙O与边AB交于异于点B的另外一点D,若⊙O的直径为5,BC=4;求DE的长.(如果用尺规作图画不出图形,可画出草图完成(2)问)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线x=1,将此抛物线向右平移1个单位,再向下平移2个单位,得到的抛物线过点( )
A. (3,6) B. (3,﹣2) C. (3,1) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
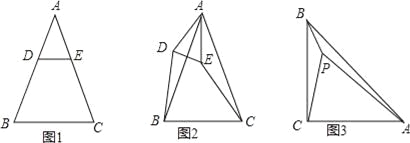
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10![]() 海里,求AC的距离.(结果保留根号)
海里,求AC的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是方程x2﹣(k﹣2)x+k2+3k+5=0的两个实数根,则x12+x22的最大值是( )
A. 19 B. 18 C. 15 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
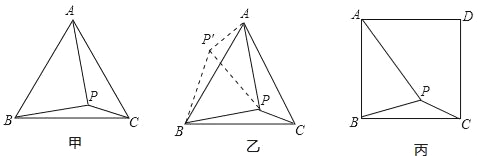
【题目】如图甲,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1,求∠BPC度数的大小和等边三角形ABC的边长.
解题思路是:将△BPC绕点B逆时针旋转60°,如图乙所示,连接PP′.
(1)△P′PB是 三角形,△PP′A是 三角形,∠BPC= °;
(2)利用△BPC可以求出△ABC的边长为 .
如图丙,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1;
,PC=1;
(3)求∠BPC度数的大小;
(4)求正方形ABCD的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com