
【题目】若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线x=1,将此抛物线向右平移1个单位,再向下平移2个单位,得到的抛物线过点( )
A. (3,6) B. (3,﹣2) C. (3,1) D. (3,2)
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
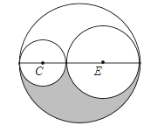
【题目】如图所示,两个小圆的半径分别是2厘米和3厘米,最外侧大圆的面积是半径为2厘米的小圆面积的几倍?阴影部分的面积是半径为3厘米的圆的面积的多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
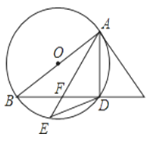
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.

(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
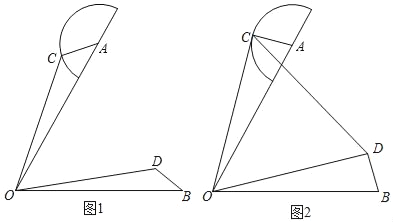
【题目】已知OA=OB=4,∠AOB=60°,半⊙A的半径为1,点C是半圆上任意一点,连结OC,把OC绕点O顺时针旋转6
0°到OD的位置,连结BD.
(1)如图1,求证:AC=BD.
(2)如图2,当OC与半圆相切于点C时,求CD的长.
(3)直接写出△AOC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②![]() =
=![]() ;③DP2=PHPB;④tan∠DBE=2﹣
;③DP2=PHPB;④tan∠DBE=2﹣![]() .
.
其中正确的是( )

A.①②③④ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
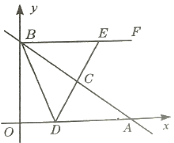
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一动点(不与
上一动点(不与![]() 点重合),射线
点重合),射线![]() 轴,延长
轴,延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,记
,记![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)是否存在![]() 的值,使得
的值,使得![]() 是以
是以![]() 为腰的等腰三角形?若存在,求出所有符合条件的
为腰的等腰三角形?若存在,求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com