
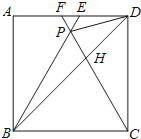
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②![]() =
=![]() ;③DP2=PHPB;④tan∠DBE=2﹣
;③DP2=PHPB;④tan∠DBE=2﹣![]() .
.
其中正确的是( )

A.①②③④ B.①②④ C.②③④ D.①③④
【答案】D
【解析】
试题分析:根据等边三角形的性质和正方形的性质,得到∠PCD=30°,于是得到∠CPD=∠CDP=75°,证得∠EDP=∠PBD=15°,于是得到△BDE∽△DPE,故①正确由于∠FDP=∠PBD,∠DFP=∠BPC=60°,推出△DFP∽△BPH,得到![]() =
=![]() =
=![]() 故②错误;由于∠PDH=∠PCD=30°,∠DPH=∠DPC,推出△DPH∽△CPD,得到
故②错误;由于∠PDH=∠PCD=30°,∠DPH=∠DPC,推出△DPH∽△CPD,得到![]() ,PB=CD,等量代换得到PD2=PHPB,故③正确;过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,于是得到∠PBC=∠PCB=60°,PB=PC=BC=CD=4,求得∠PCD=30°,根据三角函数的定义得到CM=PN=PBsin60°=4×
,PB=CD,等量代换得到PD2=PHPB,故③正确;过P作PM⊥CD,PN⊥BC,设正方形ABCD的边长是4,△BPC为正三角形,于是得到∠PBC=∠PCB=60°,PB=PC=BC=CD=4,求得∠PCD=30°,根据三角函数的定义得到CM=PN=PBsin60°=4×![]() =2
=2![]() ,PM=PCsin30°=2,由平行线的性质得到∠EDP=∠DPM,等量代换得到∠DBE=∠DPM,于是求得tan∠DBE=tan∠DPM=
,PM=PCsin30°=2,由平行线的性质得到∠EDP=∠DPM,等量代换得到∠DBE=∠DPM,于是求得tan∠DBE=tan∠DPM=![]() =
=![]() =2﹣
=2﹣![]() ,故④正确.
,故④正确.
解:∵△BPC是等边三角形,
∴BP=PC=BC,∠PBC=∠PCB=∠BPC=60°,
在正方形ABCD中,
∵AB=BC=CD,∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°,
∴∠CPD=∠CDP=75°,∴∠PDE=15°,
∵∠PBD=∠PBC﹣∠HBC=60°﹣45°=15°,
∴∠EBD=∠EDP,
∵∠DEP=∠DEB,
∴△BDE∽△DPE;故①正确;
∵PC=CD,∠PCD=30°,
∴∠PDC=75°,
∴∠FDP=15°,
∵∠DBA=45°,
∴∠PBD=15°,
∴∠FDP=∠PBD,
∵∠DFP=∠BPC=60°,
∴△DFP∽△BPH,
∴![]() =
=![]() =
=![]() =
=![]() ,故②错误;
,故②错误;
∵∠PDH=∠PCD=30°,
∵∠DPH=∠DPC,
∴△DPH∽△CDP,
∴![]() =
=![]() ,
,
∴PD2=PHCD,
∵PB=CD,
∴PD2=PHPB,故③正确;
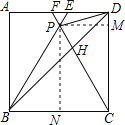
如图,过P作PM⊥CD,PN⊥BC,
设正方形ABCD的边长是4,△BPC为正三角形,
∴∠PBC=∠PCB=60°,PB=PC=BC=CD4,
∴∠PCD=30°
∴CM=PN=PBsin60°=4×![]() =2
=2![]() ,PM=PCsin30°=2,
,PM=PCsin30°=2,
∵DE∥PM,
∴∠EDP=∠DPM,
∴∠DBE=∠DPM,
∴tan∠DBE=tan∠DPM=![]() =
=![]() =2﹣
=2﹣![]() ,故④正确;
,故④正确;
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个。已知每个玩具的固定成本为360元.设每个玩具降价x元,请解决下列问题:
(1)降价后该玩具的日销售量为多少个,每个玩具盈利多少元;(用含x的代数式表示)
(2)若上述条件不变,每个玩具降价多少元时,厂家每天可获利润20000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
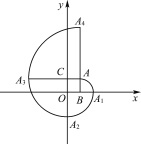
【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),![]() 是以点B为圆心,BA为半径的圆弧;
是以点B为圆心,BA为半径的圆弧;![]() 是以点O为圆心,OA1为半径的圆弧,
是以点O为圆心,OA1为半径的圆弧,![]() 是以点C为圆心,CA2为半径的圆弧,
是以点C为圆心,CA2为半径的圆弧,![]() 是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点A2 018的坐标是________.
是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点A2 018的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线x=1,将此抛物线向右平移1个单位,再向下平移2个单位,得到的抛物线过点( )
A. (3,6) B. (3,﹣2) C. (3,1) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
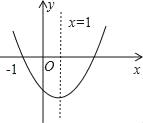
A. c<0
B. y的最小值为负值
C. 当x>1时,y随x的增大而减小
D. x=3是关于x的方程ax2+bx+c=0的一个根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10![]() 海里,求AC的距离.(结果保留根号)
海里,求AC的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
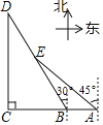
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
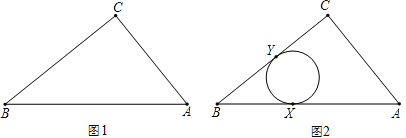
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
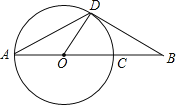
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与弧AD围成的扇形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com