
【题目】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
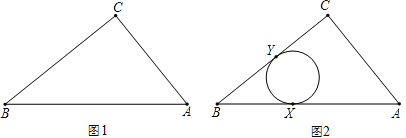
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
【答案】(1)作图见解析;(2)![]() .
.
【解析】
试题(1)作出∠B的角平分线BD,再过X作OX⊥AB,交BD于点O,则O点即为⊙O的圆心;
(2)由于⊙P与△ABC哪两条边相切不能确定,故应分⊙P与Rt△ABC的边AB和BC相切;⊙P与Rt△ABC的边AB和AC相切时;⊙P与Rt△ABC的边BC和AC相切时三种情况进行讨论.
试题解析:(1)如图所示:
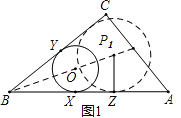
①以B为圆心,以任意长为半径画圆,分别交BC、AB于点G、H;②分别以G、H为圆心,以大于![]() GH为半径画圆,两圆相交于D,连接BD;③过X作OX⊥AB,交直线BD于点O,则点O即为⊙O的圆心.
GH为半径画圆,两圆相交于D,连接BD;③过X作OX⊥AB,交直线BD于点O,则点O即为⊙O的圆心.
(2)①当⊙P与Rt△ABC的边AB和BC相切时,由角平分线的性质可知,动点P是∠ABC的平分线BM上的点,如图1,在∠ABC的平分线BM上任意确定点P1(不为∠ABC的顶点)
∵OX=BOsin∠ABM,P1Z=BPsin∠ABM,当BP1>BO时,P1Z>OX即P与B的距离越大,⊙P的面积越大,这时,BM与AC的交点P是符合题意的、BP长度最大的点; 如图2,
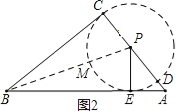
∵∠BPA>90°,过点P作PE⊥AB,垂足为E,则E在边AB上,
∴以P为圆心、PC为半径作圆,则⊙P与CB相切于C,与边AB相切于E,即这时⊙P是符合题意的圆,
时⊙P的面积就是S的最大值,
∵AC=1,BC=2,∴AB=![]() ,
,
设PC=x,则PA=AC-PC=1-x
在直角△APE中,PA2=PE2+AE2,
∴(1-x)2=x2+(![]() -2)2,
-2)2,
∴x=2![]() -4;
-4;
②如图3,
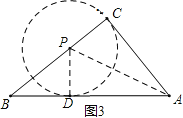
同理可得:当⊙P与Rt△ABC的边AB和AC相切时,设PC=y,则(2-y)2=y2+(![]() -1)2,
-1)2,
∴y=![]() ;
;
③如图4,
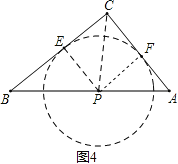
同理可得,当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,
∵△APF∽△PBE,
∴PF:BE=AF:PE,
∴![]() ,
,
∴z=![]() .
.
由①、②、③可知,
![]() >
>![]() >
>![]()
∴z>y>x,
∴⊙P的面积S的最大值为![]() π.
π.
考点:1. 切线的性质;2.角平分线的性质;3.勾股定理;4.作图—复杂作图.


科目:初中数学 来源: 题型:
【题目】某体育休闲超市购进一种成本为![]() 元/个的风筝,据市场调查分析,若按
元/个的风筝,据市场调查分析,若按![]() 元/个销售,一个月能售出
元/个销售,一个月能售出![]() 个,在此基础上,售价每涨
个,在此基础上,售价每涨![]() 元/个,月销售量就减少
元/个,月销售量就减少![]() 个.设这种风筝的销售单价为
个.设这种风筝的销售单价为![]() (元/个),该超市每月销售这种风筝的所获得的利润为
(元/个),该超市每月销售这种风筝的所获得的利润为![]() (元),针对这种风筝的销售情况,请解答下列问题:
(元),针对这种风筝的销售情况,请解答下列问题:
![]() 用含
用含![]() 的代数式分别表示出每个风筝的销售利润为________元,每月卖出的风筝的个数是________个;
的代数式分别表示出每个风筝的销售利润为________元,每月卖出的风筝的个数是________个;
![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 若该超市想在每月销售这种风筝的成本不超过
若该超市想在每月销售这种风筝的成本不超过![]() 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到![]() 元,则每个风筝的售价应定为多少元?
元,则每个风筝的售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,弹性小球从P(2,0)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为P1,第二次碰到正方形的边时的点为P2…,第n次碰到正方形的边时的点为Pn,则P2020的坐标是( )
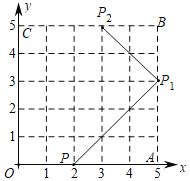
A.(5,3)B.(3,5)C.(0,2)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度,在该校随机抽取了部分学生进行问卷,问卷有以下四个选项:A.十分了解;B.了解较多:C.了解较少:D.不了解(要求:每名被调查的学生必选且只能选择一项).现将调查的结果绘制成两幅不完整的统计图.请根据两幅统计图中的信息回答下列问题:
(1)本次被抽取的学生共有_______名;
(2)请补全条形图;
(3)扇形图中的选项“C.了解较少”部分所占扇形的圆心角的大小为_______°;
(4)若该校共有![]() 名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
名学生,请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与之间的函数图象是( )
A.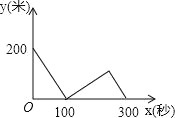 B.
B.
C.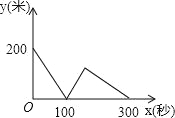 D.
D.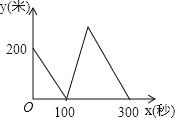
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y= kx +b的图像如图所示,看图填空:
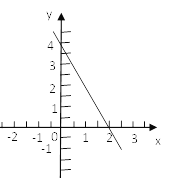
(1)当x=0时,y= ;当x= 时,y=0
(2)k= ,b= .
(3)当y=30时,x= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com