
【题目】一次函数y= kx +b的图像如图所示,看图填空:
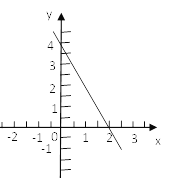
(1)当x=0时,y= ;当x= 时,y=0
(2)k= ,b= .
(3)当y=30时,x= .
【答案】(1)4,2;(2)-2,4;(3)-13
【解析】
(1)根据函数图象直接解答即可;
(2)设出函数解析式,求出k、b的值即可;
(3)根据(2)中k、b的值可求出函数解析式,再把y=30代入函数解析式,求出对应的未知数的值即可.
(1)由函数图象与坐标轴的交点可知,当x=0时,y=4;当x=4时,y=0;
故答案为:4;2;
(2)由函数的图象可知,图象与两坐标轴的交点坐标为(0,4),(2,0),
设函数的解析式为y=kx+b(k≠0),
把(0,4),(2,0)代入得,
![]() ,解得b=4,k=2;
,解得b=4,k=2;
故答案为:-2;4;
(3)由(2)可知此函数的解析式为y=2x+4,
当y=30时,即30=2x+4,解得x=13.
故答案为:-13.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+b.
(1)它的图像与两坐标轴所围成的图形的面积等于4,求b的值;
(2)它的图像经过一次函数y=-2x+1、y=x+4图像的交点,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
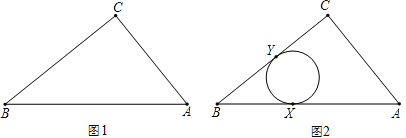
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
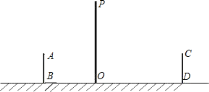
【题目】如图,是小亮晚上在广场散步的示意图,图中线段![]() 表示站立在广场上的小亮,线段
表示站立在广场上的小亮,线段![]() 表示直立在广场上的灯杆,点
表示直立在广场上的灯杆,点![]() 表示照明灯的位置.
表示照明灯的位置.
![]() 在小亮由
在小亮由![]() 处沿
处沿![]() 所在的方向行走到达
所在的方向行走到达![]() 处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在
处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在![]() 处的影子
处的影子![]() ;
;
![]() 当小亮离开灯杆的距离
当小亮离开灯杆的距离![]() 时,身高为
时,身高为![]() 的小亮的影长为
的小亮的影长为![]() ,
,
①灯杆的高度为多少![]() ?
?
②当小亮离开灯杆的距离![]() 时,小亮的影长变为多少
时,小亮的影长变为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应的任务:
杨辉三角
我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民所擅长的学科”一文中谈到,我国古代数学的许多创新与发展都曾居世界前列,他说:“实际上我们祖国伟大人民在人类史上,有过无比睿智的成就.”其中“杨辉三角”就是一例.
在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,给出了二项式![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序排列)及其系数规律.
的次数由大到小的顺序排列)及其系数规律.
如图所示
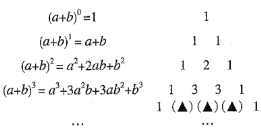
任务:(1)通过观察,图中的(▲)中可填入的数字依次为______、______、______;
(2)请直接写出![]() 的展开式:
的展开式:![]() ______;
______;
(3)根据(2)中的规律,求![]() 的值,写出计算过程.
的值,写出计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ.则:(1)∠A1=_____;(2)∠A2=_____;(3)∠An=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
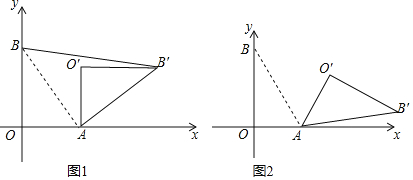
【题目】在平面直角坐标系中,O为原点,点A(3,0),点B(0,4),把△ABO绕点A顺时针旋转,得△AB′O′,点B,O旋转后的对应点为B′,O.
(1)如图1,当旋转角为90°时,求BB′的长;
(2)如图2,当旋转角为120°时,求点O′的坐标;
(3)在(2)的条件下,边OB上的一点P旋转后的对应点为P′,当O′P+AP′取得最小值时,求点P′的坐标.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】创新需要每个人的参与,就拿小华来说,为了解决晒衣服的,聪明的他想到了一个好办法,在家宽敞的院内地面![]() 上立两根等长的立柱
上立两根等长的立柱![]() 、
、![]() (均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线
(均与地面垂直),并在立柱之间悬挂一根绳子.由于挂的衣服比较多,绳子的形状近似成了抛物线![]() ,如图
,如图![]() ,已知立柱
,已知立柱![]() 米,
米, ![]() 米.
米.
(1)求绳子最低点离地面的距离;
(2)为了防止衣服碰到地面,小华在离![]() 为
为![]() 米的位置处用一根垂直于地面的立柱
米的位置处用一根垂直于地面的立柱![]() 撑起绳子 (如图2),使左边抛物线
撑起绳子 (如图2),使左边抛物线![]() 的最低点距
的最低点距![]() 为
为![]() 米,离地面
米,离地面![]() 米,求
米,求![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com