
分析 因为新添的数字就是所擦三数之和的个位数字,所以这1998个自然数的个位数字的和不变,经计算为1,又因为其它数都擦掉了,只余25和另一个数,所以另一个数就是擦掉的三数之和的个位数,从而得结论.
解答 解:∵1+2+3+…+1998=$\frac{1998×(1998+1)}{2}$=1999×999,
∴这1998个自然数的和的个位数为1,
∵其它数都擦掉了,只余25和另一个数,
∴另一个数是擦掉的三个数之和的个位数,必小于10,且与25之和的个位数为1,
所以另一个数为6.
点评 本题是数字类的变化题,此类题变化多样,要认真观察、仔细思考,善用联想是解决这类问题的方法;但本题要注意理解“写上所擦掉三个数之和的个位数字“,因此要计算1998个自然数的和,确定其个位数字,就是这1998个自然数的个位数字的和,根据这个结论计算出另一个数.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
 如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.
如图,已知在△ABC中,DE∥BC,交AC于点F,H为BC上一点,连接DH,交AC的延长线于点M,连接EH,EH与AC交于点O.若∠ADF=∠EHC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
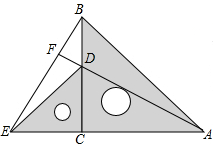 把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.
把两个含有45°角的大小不同的直角三角板如图放置,点D在BC上,连接BE,AD,AD的延长线交BE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
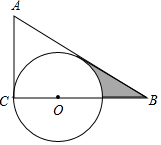 已知:如图,△ABC的∠A=60°,∠ACB=90°,BC=3,点O在BC上,且OC=1,以O为圆心,OC的半径作⊙O.
已知:如图,△ABC的∠A=60°,∠ACB=90°,BC=3,点O在BC上,且OC=1,以O为圆心,OC的半径作⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
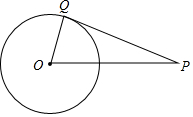 如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切
如图,点Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否相切查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com