Question

1．如图1，在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（n，0）且a、n满足|a+2|+$\sqrt{5-n}$=0，现同时将点A，B分别向上平移4个单位，再向右平移3个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及四边形OBDC的面积；
（2）如图2，若 点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）$\frac{∠DCP+∠BOP}{∠CPO}$的值是否发生变化，并说明理由．
（3）在四边形OBDC内是否存在一点P，连接PO，PB，PC，PD，使S_△PCD=S_△PBD； S_△POB：S_△POC=1？若存在这样一点，求出点P的坐标，若不存在，试说明理由．

Answer 1

分析 （1）根据被开方数和绝对值大于等于0列式求出b和n，从而得到A、B的坐标，再根据向上平移4个单位，则纵坐标加4，向右平移3个单位，则横坐标加3，求出点C、D的坐标即可，然后利用平行四边形的面积公式，列式计算；
（2）根据平移的性质可得AB∥CD，再过点P作PE∥AB，根据平行公理可得PE∥CD，然后根据两直线平行，内错角相等可得∠DCP=∠CPE，∠BOP=∠OPE，然后求出∠CPO=∠DCP+∠BOP，从而判断出比值不变；
（3）根据面积相等的特殊性可知，点P为平行四边形ABCD对角线的交点，即PB=PC，因此根据中点可求出点P的坐标．

解答 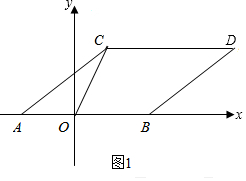解：（1）如图1，
由题意得，a+2=0，a=-2，则A（-2，0），
5-n=0，n=5，则B（5，0），
∵点A，B分别向上平移4个单位，再向右平移3个单位，
∴点C（1，4），D（8，4）；
∵OB=5，CD=8-1=7，
∴S_{四边形OBDC}=$\frac{1}{2}$（CD+OB）×h=$\frac{1}{2}$×4×（5+7）=24；
（2）$\frac{∠DCP+∠BOP}{∠CPO}$的值不发生变化，且值为1，理由是：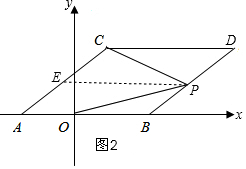
由平移的性质可得AB∥CD，
如图2，过点P作PE∥AB，交AC于E，则PE∥CD，
∴∠DCP=∠CPE，∠BOP=∠OPE，
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP，
∴$\frac{∠DCP+∠BOP}{∠CPO}$=1，比值不变．

（3）存在，如图3，连接AD和BC交于点P，
∵AB=CD，AB∥CD，
∴四边形ABCD是平行四边形，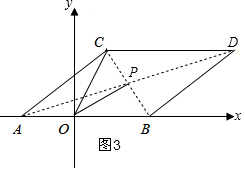
∴BP=CP，
∴S_△PCD=S_△PBD； S_△POB：S_△POC=1，
∵C（1，4），B（5，0）
∴P（3，2）．

点评 本题是几何变换的综合题，考查了线段平移与点的坐标的关系，明确点的坐标的平移原则：①上移→纵+，②下移→纵-，③左移→横-，④右移→横+；同时对于面积的关系除了熟记面积公式外，要知道三角形的中线把三角形分成面积相等的两个三角形；第二问中角的比值的证明，在几何中很少出现，不过此题分子与分母中角的大小相等，属于平行线的性质得出的结论．