
【题目】如图,在同一平面内,将两个全等的等腰直角三角形![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,它们的斜边长为2,若
,它们的斜边长为2,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合),设
重合),设![]() ,
,![]() .
.
(1)请在图(1)中找出两对相似但不全等的三角形,并选取其中一对进行证明.
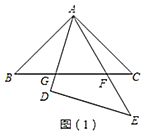
(2)求![]() 与a的函数关系式,直接写出自变量a的取值范围.
与a的函数关系式,直接写出自变量a的取值范围.
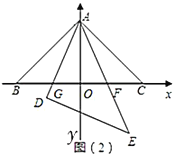
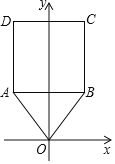
(3)以![]() 的斜边
的斜边![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 边上的高所在的直线为
边上的高所在的直线为![]() 轴,建立平面直角坐标系如图(2),若
轴,建立平面直角坐标系如图(2),若![]() ,求出点
,求出点![]() 的坐标,猜想线段
的坐标,猜想线段![]() 、
、![]() 和
和![]() 之间的关系,并通过计算加以验证.
之间的关系,并通过计算加以验证.
【答案】(1)△ACG∽△FAG,△FAG∽△FBA,证明见解析;(2)b=![]() ,1<a<2;(3)G(1-
,1<a<2;(3)G(1-![]() ,0);BG2+CF2=FG2.
,0);BG2+CF2=FG2.
【解析】
(1)找到有公共角的和45°角的两个三角形即可;
(2)证明△ACG∽△FBA,利用相似三角形的对应边成比例可得![]() 与a的函数关系式,根据点F与点C重合时a为2,点G与点B重合时a为1,可得a的取值范围
与a的函数关系式,根据点F与点C重合时a为2,点G与点B重合时a为1,可得a的取值范围
(3)先求得a=b=![]() ,可求点G(1-
,可求点G(1-![]() ,0);根据BG=OB﹣OG,求得FG=BC﹣2BG=2
,0);根据BG=OB﹣OG,求得FG=BC﹣2BG=2![]() -2,即可得到线段
-2,即可得到线段![]() 、
、![]() 和
和![]() 之间的关系.
之间的关系.
(1)△ACG∽△FAG,△FAG∽△FBA.
∵∠GAF=∠C=45°,
∠AGF=∠AGC,
∴△ACG∽△FAG.类似证明△FAG∽△FBA;
(2)∵∠CAG=∠CAF+45°,∠BFA=∠CAF+45°,
∴∠CAG=∠BFA.
∵∠B=∠C=45°,
∴△ACG∽△FBA,
∴ ![]() =
=![]() .
.
由题意可得CA=BA=![]() .
.
∴![]() =
=![]() .∴b=
.∴b=![]() .
.
自变量a的取值范围为1<a<2.
(3)由BG=CF可得BF=CG,即a=b.
∵b=![]() ,
,
∴a=b=![]() .
.
∵OB=OC=![]() BC=1,
BC=1,
∴OF=OG=![]() ﹣1.
﹣1.
∴G(1-![]() ,0).
,0).
线段BG、FG和CF之间的关系为BG2+CF2=FG2;
∵BG=OB﹣OG=1-(![]() -1)=2-
-1)=2-![]() =CF,
=CF,
FG=BC﹣2BG= 2-2(2-![]() )=2
)=2![]() -2.
-2.
∵BG2+CF2=2(2-![]() )2=12-8
)2=12-8![]() ,FG2=(2
,FG2=(2![]() -2)2=12-8
-2)2=12-8![]() .
.
∴BG2+CF2=FG2 .


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与
的图象与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象分别交于
的图象分别交于![]() 、
、![]() 两点.
两点.
(1)如图,当![]() ,点
,点![]() 在线段
在线段![]() 上(不与点
上(不与点![]() 、
、![]() 重合)时,过点
重合)时,过点![]() 作
作![]() 轴和
轴和![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() 、
、![]() .当矩形
.当矩形![]() 的面积为2时,求出点
的面积为2时,求出点![]() 的位置;
的位置;

(2)如图,当![]() 时,在
时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;

(3)若某个等腰三角形的一条边长为5,另两条边长恰好是两个函数图象的交点横坐标,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.
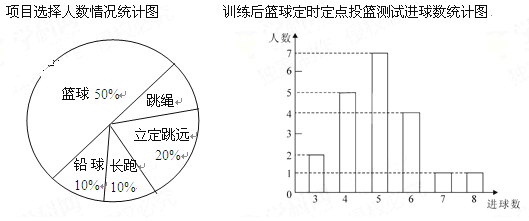
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人, 训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点.
(1)当m=﹣2时,求二次函数的图象与x轴交点的坐标;
(2)过点P(0,m﹣1)作直线1⊥y轴,二次函数图象的顶点A在直线l与x轴之间(不包含点A在直线l上),求m的范围;
(3)在(2)的条件下,设二次函数图象的对称轴与直线l相交于点B,求△ABO的面积最大时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() ,
,![]() 是
是![]() 的边
的边![]() 上一点.
上一点.

(1)将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,请在网格中画出
,请在网格中画出![]() ;
;
(2)将![]() 沿一定的方向平移后,点
沿一定的方向平移后,点![]() 的对应点为
的对应点为![]() ,请在网格中画出上述平移后的
,请在网格中画出上述平移后的![]() ,并写出点
,并写出点![]() 的坐标:
的坐标:![]() ( );
( );
(3)若以点![]() 为位似中心,作
为位似中心,作![]() 与
与![]() 成
成![]() 的位似,则与点
的位似,则与点![]() 对应的点
对应的点![]() 位似坐标为______(不用作图,直接写出结果).
位似坐标为______(不用作图,直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织首届“数学文化节”活动,旨在引导同学们感受数学魅力,提升数学素养,活动中,九年级全体同学参加了“趣味数学知识竞赛”.活动中获得“数学之星”称号的小颖得到了![]() 四枚纪念章,(除头像外完全相同),如图所示,四枚纪念章上分别印有四位数学家的头像,她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹,求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率.(提示:答题时可用序号
四枚纪念章,(除头像外完全相同),如图所示,四枚纪念章上分别印有四位数学家的头像,她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹,求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率.(提示:答题时可用序号![]() 表示相应的纪念章)
表示相应的纪念章)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,顶点O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O逆时针旋转,每次旋转90°,则第2019次旋转结束时,点D的坐标为( )
A.(3,﹣10)B.(10,3)C.(﹣10,﹣3)D.(10,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y=![]() x2﹣
x2﹣![]() x+3的绳子.
x+3的绳子.

(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com