
°ĺŐ‚ńŅ°Ņ“—÷™“ĽīőļĮ ż![]() ĶńÕľŌů”Ž
ĶńÕľŌů”Ž![]() ÷ŠļÕ
÷ŠļÕ![]() ÷Š∑÷ĪūĹĽ”ŕ
÷Š∑÷ĪūĹĽ”ŕ![]() °Ę
°Ę![]() ŃĹĶ„£¨”Ž∑īĪ»ņżļĮ ż
ŃĹĶ„£¨”Ž∑īĪ»ņżļĮ ż![]() ĶńÕľŌů∑÷ĪūĹĽ”ŕ
ĶńÕľŌů∑÷ĪūĹĽ”ŕ![]() °Ę
°Ę![]() ŃĹĶ„£ģ
ŃĹĶ„£ģ
£®1£©»ÁÕľ£¨ĶĪ![]() £¨Ķ„
£¨Ķ„![]() ‘ŕŌŖ∂ő
‘ŕŌŖ∂ő![]() …Ō£®≤Ľ”ŽĶ„
…Ō£®≤Ľ”ŽĶ„![]() °Ę
°Ę![]() ÷ōļŌ£© Ī£¨ĻżĶ„
÷ōļŌ£© Ī£¨ĻżĶ„![]() ◊ų
◊ų![]() ÷ŠļÕ
÷ŠļÕ![]() ÷ŠĶńīĻŌŖ£¨īĻ◊„ő™
÷ŠĶńīĻŌŖ£¨īĻ◊„ő™![]() °Ę
°Ę![]() £ģĶĪĺō–ő
£ģĶĪĺō–ő![]() Ķń√śĽżő™2 Ī£¨«ů≥ŲĶ„
Ķń√śĽżő™2 Ī£¨«ů≥ŲĶ„![]() ĶńőĽ÷√£Ľ
ĶńőĽ÷√£Ľ

£®2£©»ÁÕľ£¨ĶĪ![]() Ī£¨‘ŕ
Ī£¨‘ŕ![]() ÷Š…Ō «∑Ůīś‘ŕĶ„
÷Š…Ō «∑Ůīś‘ŕĶ„![]() £¨ ĻĶ√“‘
£¨ ĻĶ√“‘![]() °Ę
°Ę![]() °Ę
°Ę![]() ő™∂•Ķ„Ķń»żĹ«–ő”Ž
ő™∂•Ķ„Ķń»żĹ«–ő”Ž![]() Ōŗň∆£Ņ»Űīś‘ŕ£¨«ů≥ŲĶ„
Ōŗň∆£Ņ»Űīś‘ŕ£¨«ů≥ŲĶ„![]() Ķń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£Ľ
Ķń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£Ľ

£®3£©»Űń≥łŲĶ»—Ł»żĹ«–őĶń“ĽŐűĪŖ≥§ő™5£¨ŃŪŃĹŐűĪŖ≥§«°ļ√ «ŃĹłŲļĮ żÕľŌůĶńĹĽĶ„ļŠ◊ÝĪÍ£¨«ů![]() Ķń÷Ķ£ģ
Ķń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©![]() ĽÚ
ĽÚ![]() £Ľ£®2£©īś‘ŕ£¨
£Ľ£®2£©īś‘ŕ£¨![]() ĽÚ
ĽÚ![]() £Ľ£®3£©
£Ľ£®3£©![]()
°ĺĹ‚őŲ°Ņ
£®1£©łý囓—÷™ŐűľĢŌ»«ů≥ŲļĮ żĹ‚őŲ Ĺ£¨»Ľļůłýĺ›∆Ĺ––Ķ√ĶĹ![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨”÷ĹŠļŌĺō–ő√śĽż=
£¨”÷ĹŠļŌĺō–ő√śĽż=![]() £¨Ņ…«ů≥ŲĹŠĻŻ£Ľ
£¨Ņ…«ů≥ŲĹŠĻŻ£Ľ
£®2£©Ō»”…“—÷™ŐűľĢÕ∆ĶĹ≥ŲĶ„E‘ŕAĶ„◊ů≤ŗ£¨»Ľļů«ů≥ŲC,DŃĹĶ„◊ÝĪÍ£¨‘Ŕ∑÷“‘Ō¬ŃĹ÷÷«ťŅŲ£ļĘŔĶĪ![]() £ĽĘŕĶĪ
£ĽĘŕĶĪ![]() £¨Ķ√≥Ų
£¨Ķ√≥Ų![]() £¨ĹÝ∂ÝŅ…Ķ√≥ŲĹŠĻŻ£Ľ
£¨ĹÝ∂ÝŅ…Ķ√≥ŲĹŠĻŻ£Ľ
£®3£©Ń™ŃĘ“ĽīőļĮ żļÕ∑īĪ»ņżļĮ żĶńĹ‚őŲ ĹĶ√≥Ų∑Ĺ≥Ő◊ť£¨ŌŻ»•yĶ√≥ŲĻō”ŕxĶń“Ľ‘™∂Ģīő∑Ĺ≥Ő£¨Ĺ‚≥ŲxĶń÷Ķ£¨‘Ŕ∑÷“‘Ō¬ŃĹ÷÷«ťŅŲĹŠļŌ»żĹ«–őĶń»żĪŖĻōŌĶ«ůĹ‚£ļĘŔ5ő™Ķ»—Ł»żĹ«–őĶń—Ł≥§£Ľ
Ęŕ5ő™Ķ»—Ł»żĹ«–őĶ◊ĪŖ≥§.ĹÝ∂ÝĶ√≥ŲkĶń÷Ķ.
Ĺ‚£ļ£®1£©ĶĪ![]() Ī£¨
Ī£¨![]() £¨
£¨
»ÁÕľ£¨”…![]() ÷Š£¨
÷Š£¨![]() ÷Š£¨“◊Ķ√
÷Š£¨“◊Ķ√![]() £ģ
£ģ
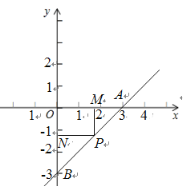
°ŗ![]() £¨ľī
£¨ľī![]() ĘŔ£¨
ĘŔ£¨
∂Ýĺō–ő√śĽżő™2£¨°ŗ![]() Ęŕ.
Ęŕ.
°ŗ”…ĘŔĘŕĶ√![]() ő™1ĽÚ2.
ő™1ĽÚ2.
°ŗ![]() ĽÚ
ĽÚ![]() .
.
£®2£©°Ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ![]() £¨∂Ý
£¨∂Ý![]() £¨
£¨
°ŗ![]() Ķ„≤ĽŅ…ń‹‘ŕ
Ķ„≤ĽŅ…ń‹‘ŕ![]() Ķ„”“≤ŗ£¨
Ķ„”“≤ŗ£¨
ĶĪ![]() ‘ŕ
‘ŕ![]() Ķ„◊ů≤ŗ Ī£¨
Ķ„◊ů≤ŗ Ī£¨![]() £¨
£¨![]()
Ń™ŃĘ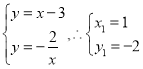 ĽÚ
ĽÚ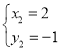
ľī![]() £¨
£¨![]() .
.
ĘŔĶĪ![]() £¨°ŗ
£¨°ŗ![]() .
.
∂Ý![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
ľī![]() .
.
°ŗ![]() .
.
ĘŕĶĪ![]() £¨°ŗ
£¨°ŗ![]() £ģ
£ģ
ľī![]() £¨°ŗ
£¨°ŗ![]() .
.
◊Ř…Ōňý Ų£¨![]() ĽÚ
ĽÚ![]() .
.
£®3£©ĶĪ![]() ļÕ
ļÕ![]() Ī£¨
Ī£¨
Ń™ŃĘ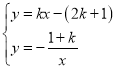 £¨
£¨
Ķ√![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨![]() .
.
ĘŔĶĪ5ő™Ķ»—Ł»żĹ«–őĶń—Ł≥§ Ī£¨![]() .
.
ĘŕĶĪ5ő™Ķ»—Ł»żĹ«–őĶ◊ĪŖ≥§ Ī£¨![]() £ģ
£ģ
∂Ý![]() £¨°ŗ…Š»•.
£¨°ŗ…Š»•.
“Úīň£¨◊Ř…Ō£¨![]() .
.



| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ![]() »° ≤√ī÷Ķ Ī£¨Ļō”ŕ
»° ≤√ī÷Ķ Ī£¨Ļō”ŕ![]() Ķń∑Ĺ≥Ő
Ķń∑Ĺ≥Ő![]() ”–ŃĹłŲŌŗĶ»Ķń Ķ żłý£Ņ«ů≥Ų’‚ Ī∑Ĺ≥ŐĶńłý.
”–ŃĹłŲŌŗĶ»Ķń Ķ żłý£Ņ«ů≥Ų’‚ Ī∑Ĺ≥ŐĶńłý.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ «∂ĢīőļĮ ży£Ĺax2+bx+cÕľŌůĶń“Ľ≤Ņ∑÷£¨ÕľŌůĻżĶ„A(©Ā3£¨0)£¨∂‘≥∆÷Šő™÷ĪŌŖx£Ĺ©Ā1£¨Ō¬Ń–ĹŠ¬Ř£ļĘŔb2£ĺ4ac£ĽĘŕ2a+b£Ĺ0£ĽĘŘa+b+c£ĺ0£ĽĘ‹»ŰB(©Ā5£¨y1)°ĘC(©Ā1£¨y2)ő™ļĮ żÕľŌů…ŌĶńŃĹĶ„£¨‘Úy1£ľy2£ģ∆š÷–’ż»∑ĹŠ¬Ř «£® £©

A.ĘŕĘ‹B.ĘŔĘŘĘ‹C.ĘŔĘ‹D.ĘŕĘŘ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņį—īů–°ļÕ–ő◊īÕÍ»ęŌŗÕ¨Ķń6’ŇŅ®∆¨∑÷≥…ŃĹ◊ť£¨√Ņ◊ť3’Ň£¨∑÷ĪūĪÍ…Ō1°Ę2°Ę3£¨Ĺę’‚ŃĹ◊ťŅ®∆¨∑÷Īū∑Ň»ŽŃĹłŲļ–◊”÷–ĹŃ‘»£¨‘Ŕī”÷–ňśĽķ≥ť»°“Ľ’Ň£ģ
£®1£© ‘«ů»°≥ŲĶńŃĹ’ŇŅ®∆¨ ż◊÷÷ģļÕő™∆ś żĶńłŇ¬ £Ľ
£®2£©»Ű»°≥ŲĶńŃĹ’ŇŅ®∆¨ ż◊÷÷ģļÕő™∆ś ż£¨‘Úľ◊ §£Ľ»°≥ŲĶńŃĹ’ŇŅ®∆¨ ż◊÷÷ģļÕő™Ňľ ż£¨‘Ú““ §£Ľ ‘∑÷őŲ’‚łŲ”őŌ∑ «∑ŮĻę∆Ĺ£Ņ«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ![]() ÷–£¨ļĮ ż
÷–£¨ļĮ ż![]() ĶńÕľŌů”ŽļĮ ż
ĶńÕľŌů”ŽļĮ ż![]() £®
£®![]() £©ĶńÕľŌůŌŗĹĽ”ŕĶ„
£©ĶńÕľŌůŌŗĹĽ”ŕĶ„![]() £¨≤Ę”Ž
£¨≤Ę”Ž![]() ÷ŠĹĽ”ŕĶ„
÷ŠĹĽ”ŕĶ„![]() £ģĶ„
£ģĶ„![]() «ŌŖ∂ő
«ŌŖ∂ő![]() …Ō“ĽĶ„£¨
…Ō“ĽĶ„£¨![]() ”Ž
”Ž![]() Ķń√śĽżĪ»ő™2£ļ3£ģ
Ķń√śĽżĪ»ő™2£ļ3£ģ
£®1£©![]() £¨
£¨![]() £Ľ
£Ľ
£®2£©«ůĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
£®3£©»ŰĹę![]() »∆Ķ„
»∆Ķ„![]() ň≥ Ī’Ž–ż◊™£¨Ķ√ĶĹ
ň≥ Ī’Ž–ż◊™£¨Ķ√ĶĹ![]() £¨∆š÷–
£¨∆š÷–![]() Ķń∂‘”¶Ķ„ «
Ķń∂‘”¶Ķ„ «![]() £¨
£¨![]() Ķń∂‘”¶Ķ„ «
Ķń∂‘”¶Ķ„ «![]() £¨ĶĪĶ„
£¨ĶĪĶ„![]() ¬š‘ŕ
¬š‘ŕ![]() ÷Š’żįŽ÷Š…Ō£¨Ň–∂ŌĶ„
÷Š’żįŽ÷Š…Ō£¨Ň–∂ŌĶ„![]() «∑٬š‘ŕļĮ ż
«∑٬š‘ŕļĮ ż![]() £®
£®![]() £©ĶńÕľŌů…Ō£¨≤ĘňĶ√ųņŪ”…£ģ
£©ĶńÕľŌů…Ō£¨≤ĘňĶ√ųņŪ”…£ģ

≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ2016ńÍ3‘¬Ļķľ ∑Áů›Ĺŕ∆ŕľš£¨Õűīů≤ģĺŲ∂®Ōķ Ř“ĽŇķ∑Áů›£¨ĺ≠ –≥°Ķų—–£ļÚýÚū–Õ∑Áů›ĹÝľŘ√ŅłŲő™10‘™£¨ĶĪ ŘľŘ√ŅłŲő™12‘™ Ī£¨Ōķ ŘŃŅő™180łŲ£¨»Ű ŘľŘ√ŅŐŠłŖ1‘™£¨Ōķ ŘŃŅĺÕĽŠľű…Ŕ10łŲ£¨«ŽĽōīū“‘Ō¬ő Ő‚£ļ
£®1£©”√ĪŪīÔ ĹĪŪ ĺÚýÚū–Õ∑Áů›Ōķ ŘŃŅy£®łŲ£©”Ž ŘľŘx£®‘™£©÷ģľšĶńļĮ żĻōŌĶ£®12°‹x°‹30£©£Ľ
£®2£©Õűīů≤ģő™Ńň»√ņŻłÝĻňŅÕ£¨≤ĘÕ¨ ĪĽŮĶ√840‘™ņŻ»ů£¨ ؾؔ¶∂®ő™∂ŗ…Ŕ£Ņ
£®3£©ĶĪ ŘľŘ∂®ő™∂ŗ…Ŕ Ī£¨Õűīů≤ģĽŮĶ√ņŻ»ůW◊Óīů£¨◊ÓīůņŻ»ů «∂ŗ…Ŕ£Ņ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
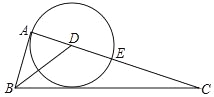
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕRt°ųABC÷–£¨°ŌBAC=90°„£¨BD «Ĺ«∆Ĺ∑÷ŌŖ£¨“‘Ķ„Dő™‘≤–ń£¨DAő™įŽĺ∂Ķń°—D”ŽACŌŗĹĽ”ŕĶ„E
£®1£©«ů÷§£ļBC «°—DĶń«–ŌŖ£Ľ
£®2£©»ŰAB=5£¨BC=13£¨«ůCEĶń≥§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥ ż—ß–ň»§–°◊ťłýĺ›—ßŌįļĮ żĶńĺ≠—ť£¨∂‘∑÷∂őļĮ ż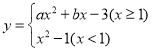 ĶńÕľŌů”Ž–‘÷ ĹÝ––ŃňŐĹĺŅ£¨«Ž≤Ļ≥šÕÍ’Ż“‘Ō¬ĶńŐĹĺŅĻż≥Ő£ģ
ĶńÕľŌů”Ž–‘÷ ĹÝ––ŃňŐĹĺŅ£¨«Ž≤Ļ≥šÕÍ’Ż“‘Ō¬ĶńŐĹĺŅĻż≥Ő£ģ
x | °≠ | £≠2 | £≠1 | 0 | 1 | 2 | 3 | 4 | °≠ |
y | °≠ | 3 | 0 | £≠1 | 0 | 1 | 0 | £≠3 | °≠ |
£®1£©ŐÓŅ’£ļa£Ĺ°° °°£ģb£Ĺ°° °°£ģ
£®2£©ĘŔłýĺ›…Ō ŲĪŪłŮ żĺ›≤Ļ»ęļĮ żÕľŌů£Ľ
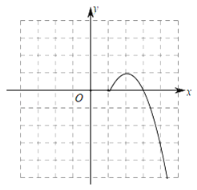
Ęŕł√ļĮ żÕľŌů «÷Š∂‘≥∆Õľ–őĽĻ «÷––ń∂‘≥∆Õľ–ő£Ņ
£®3£©»Ű÷ĪŌŖ![]() ”Žł√ļĮ żÕľŌů”–»żłŲĹĽĶ„£¨«ůtĶń»°÷Ķ∑∂őߣģ
”Žł√ļĮ żÕľŌů”–»żłŲĹĽĶ„£¨«ůtĶń»°÷Ķ∑∂őߣģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
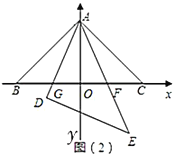
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕÕ¨“Ľ∆Ĺ√śńŕ£¨ĹęŃĹłŲ»ęĶ»ĶńĶ»—Ł÷ĪĹ«»żĹ«–ő![]() ļÕ
ļÕ![]() įŕ∑Ň‘ŕ“Ľ∆ū£¨
įŕ∑Ň‘ŕ“Ľ∆ū£¨![]() ő™ĻęĻ≤∂•Ķ„£¨
ő™ĻęĻ≤∂•Ķ„£¨![]() £¨ňŁ√«Ķń–ĪĪŖ≥§ő™2£¨»Ű
£¨ňŁ√«Ķń–ĪĪŖ≥§ő™2£¨»Ű![]() ĻŐ∂®≤Ľ∂Į£¨
ĻŐ∂®≤Ľ∂Į£¨![]() »∆Ķ„
»∆Ķ„![]() –ż◊™£¨
–ż◊™£¨![]() °Ę
°Ę![]() ”ŽĪŖ
”ŽĪŖ![]() ĶńĹĽĶ„∑÷Īūő™
ĶńĹĽĶ„∑÷Īūő™![]() °Ę
°Ę![]() £®Ķ„
£®Ķ„![]() ≤Ľ”ŽĶ„
≤Ľ”ŽĶ„![]() ÷ōļŌ£¨Ķ„
÷ōļŌ£¨Ķ„![]() ≤Ľ”ŽĶ„
≤Ľ”ŽĶ„![]() ÷ōļŌ£©£¨…Ť
÷ōļŌ£©£¨…Ť![]() £¨
£¨![]() £ģ
£ģ
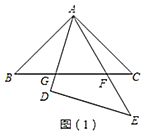
£®1£©«Ž‘ŕÕľ£®1£©÷–’“≥ŲŃĹ∂‘Ōŗň∆Ķę≤Ľ»ęĶ»Ķń»żĹ«–ő£¨≤Ę—°»°∆š÷–“Ľ∂‘ĹÝ––÷§√ų£ģ
£®2£©«ů![]() ”ŽaĶńļĮ żĻōŌĶ Ĺ£¨÷ĪĹ”–ī≥Ų◊‘ĪšŃŅaĶń»°÷Ķ∑∂őߣģ
”ŽaĶńļĮ żĻōŌĶ Ĺ£¨÷ĪĹ”–ī≥Ų◊‘ĪšŃŅaĶń»°÷Ķ∑∂őߣģ
£®3£©“‘![]() Ķń–ĪĪŖ
Ķń–ĪĪŖ![]() ňý‘ŕĶń÷ĪŌŖő™
ňý‘ŕĶń÷ĪŌŖő™![]() ÷Š£¨
÷Š£¨![]() ĪŖ…ŌĶńłŖňý‘ŕĶń÷ĪŌŖő™
ĪŖ…ŌĶńłŖňý‘ŕĶń÷ĪŌŖő™![]() ÷Š£¨Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ»ÁÕľ£®2£©£¨»Ű
÷Š£¨Ĺ®ŃĘ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ»ÁÕľ£®2£©£¨»Ű![]() £¨«ů≥ŲĶ„
£¨«ů≥ŲĶ„![]() Ķń◊ÝĪÍ£¨≤¬ŌŽŌŖ∂ő
Ķń◊ÝĪÍ£¨≤¬ŌŽŌŖ∂ő![]() °Ę
°Ę![]() ļÕ
ļÕ![]() ÷ģľšĶńĻōŌĶ£¨≤ĘÕ®Ļżľ∆ň„ľ”“‘—ť÷§£ģ
÷ģľšĶńĻōŌĶ£¨≤ĘÕ®Ļżľ∆ň„ľ”“‘—ť÷§£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com