
【题目】如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积. 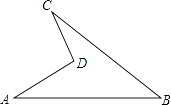
【答案】解:连接AC, 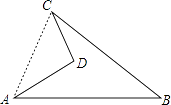
∵CD⊥AD
∴∠ADC=90°,
∵AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2 ,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC﹣S△ADC=30﹣6=24m2 .
【解析】连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣mx﹣2m2=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若x=1是该方程的根,求代数式4m2+2m+5的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝店专销某种品牌的运动服,每套进价70元,售价120元/套.为了促销,淘宝店决定凡是一次购买数量不超过10套的,按原价每套120元购买;10套以上的,每多买1套,每套降价1元,每多买2套,每套降价2元…^(例如,某人一次性购买15套运动服,多出5套,按每套降价5元购买,共需(15×115)元;但是最低价90元/套.
(1)求顾客一次至少买多少套,才能以最低价购买?,
(2)写出当一次购买![]() (
(![]() >10)件时,利润
>10)件时,利润![]() (元)与购买量
(元)与购买量![]() (件)之间的函数关系式;
(件)之间的函数关系式;
(3)有一天,一位顾客买了35套运动服,另一位顾客买了40套运动服,淘宝店发现卖了40套反而比卖35套赚的钱少!为了使每次卖的数量多赚的钱也多,在其它促销条件不变的情况下,最低价为90元/套至少要提高到多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.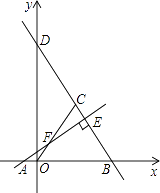
(1)求直线BD的函数表达式;
(2)求线段OF的长;
(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com