
【题目】如图,△ABC中,E为AD与CF的交点,AE=ED,已知△ABC的面积是1,△BEF的面积是 ![]() ,则△AEF的面积是;
,则△AEF的面积是;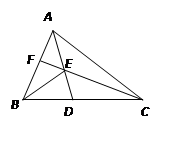
【答案】![]()
【解析】解:作AM⊥BC于M,EN⊥BC于N,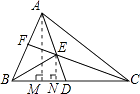
则EN∥AM,ED:AD=EN:AM,
∵AE=ED,
∴AD=2AE,
∴AM=2EN,
作AM⊥BC于M,EN⊥BC于N,得出EN∥AM,
∴S△ABC= ![]() BCAM,S△EBC=
BCAM,S△EBC= ![]() BCEN,
BCEN,
∴S△EBC= ![]() S△ABC又∵S△BEF=
S△ABC又∵S△BEF= ![]()
∴S△FBC=S△EBC+S△BEF= ![]() +
+ ![]() =
= ![]()
∴S△AFC=S△ABC-S△FBC=1- ![]() =
= ![]()
分别将AF和BF看做S△AFC和S△FBC的底,由于两个三角形的高相同,
∴AF:FB=S△AFC:S△FBC= ![]() :
: ![]() =2:3
=2:3
,
分别将AF和BF看做S△AFE和S△FBE的底,由于两个三角形的高相同
∴S△AFE:S△BEF=AF:FB=2:3,
∴S△AFE= ![]() ×
× ![]() =
= ![]()
根据平行线分线段成比例及线段中点的定义证得AM=2EN,可得到△EBC的面积等于△ABC面积的一半,再根据S△FBC=S△EBC+S△BEF及△ABC的面积是1,△BEF的面积是 ![]() , 求出△FBC的面积,再根据S△AFC=S△ABC-S△FBC , 就可求出△AFC的面积,然后根据S△AFC和S△FBC两个三角形的高相同,求出底边之比,根据S△AFE:S△BEF=AF:FB=2:3,即可求出答案。
, 求出△FBC的面积,再根据S△AFC=S△ABC-S△FBC , 就可求出△AFC的面积,然后根据S△AFC和S△FBC两个三角形的高相同,求出底边之比,根据S△AFE:S△BEF=AF:FB=2:3,即可求出答案。


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.
(1)写出两个不全等且与△GHC相似的三角形,并任选其中的一个进行证明;
(2)求GH的长.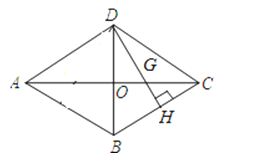
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校去年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2400元,购买乙种足球共花费1600元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元.
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)今年学校为编排“足球操”,决定再次购买甲、乙两种足球共50个.如果两种足球的单价没有改变,而此次购买甲、乙两种足球的总费用不超过3500元,那么这所学校最少可购买多少个甲种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,E是BC边上一点,只用一把无刻度的直尺在AD边上作点F,使得DF=BE.
(1)作出满足题意的点F,简要说明你的作图过程;
(2)依据你的作图,证明:DF=BE.
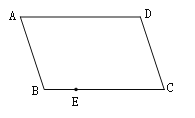
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com