
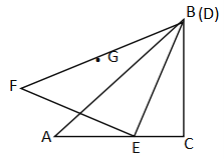
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=![]() .点D,E分别在边AB,AC上,将线段ED绕点E按逆时针方向旋转90°得到EF,连结BF,BF的中点为G.
.点D,E分别在边AB,AC上,将线段ED绕点E按逆时针方向旋转90°得到EF,连结BF,BF的中点为G.
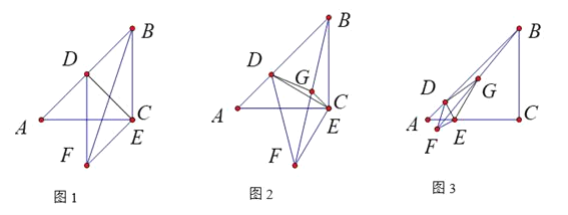
(1)当点E与点C重合时.
①如图1,若AD=BD,求BF的长.
②当点D从点A运动到点B时,求点G的运动路径长.
(2)当AE=3,点G在△DEF一边所在直线上时,求AD的长.
【答案】(1)①![]() ;②
;②![]()
(2)![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)①利用等腰直角三角形的性质,易证AC=BC,∠A=45°,利用解直角三角形求出AC,BC的长,利用旋转的性质,可证得△DCF是等腰直角三角形,从而可求出DF的长,再证明DF∥BC,可得到四边形DFCB是平行四边形,利用平行四边形的对角线的性质,可证得BF=2GF,DC=2CG,继而可求出CG的长,然后利用勾股定理求出GF的长,从而可求出BF的长;②如图,连接AF,取AB的中点T,连接GT,利用等腰直角三角形的性质,可证得CA=CB,CD=CF,∠ACB=∠DCF=90°,∠CAB=45°,利用SAS证明△ACF≌△BCD,利用全等三角形的性质可得到∠CAF=∠CBD=45°,AF=BD,从而可证AF⊥AB,即可得到TG∥AF,就可推出TG⊥AB,由此可得点G的运动轨迹是Rt△ABC斜边的中线,即可求出点G的运动路径长.
(2)分情况讨论:当点G在直线EF上时,过点D作DJ⊥AC于点J,设AJ=DJ=x,则EJ=3-x,易证△DEJ∽△EBC,利用相似三角形的对应边成比例建立关于x的方程,解方程求出x的值,可得到AJ,DJ的长,在等腰直角△ADJ中,利用解直角三角形求出AD的长;当点G在直线DF上时,利用解直角三角形求出AD的长;当点G在直线DE上时,过点F作FT⊥CA交CA的延长线于点T,过点G作GK⊥AC于点K,过点D作DJ⊥AC于点J,设FT=AT=y,用含y的代数式表示出KG,EK的长,再证明△FET∽△EGK,利用相似三角形的对应边成比例,建立关于y的方程,解方程求出y的值,就可得到TF,TE的长,然后求出DJ的长,利用解直角三角形求出AD的长;当点G在直线DF上时,点D与点B重合,求出AD的长即可.
(1)解:如图,
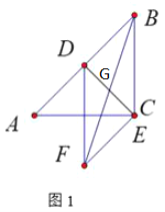
①当点E与点C重合时.
∵△ABC是等腰直角三角形,
∴AC=BC,∠A=45°,
∴AC=BC=ABsin∠A=![]() sin45°=
sin45°=![]() ;
;
∵将线段ED绕点E按逆时针方向旋转90°得到EF,
∴∠DCE=90°,DE=CF
∴△DCF是等腰直角三角形,
∵AD=CD=CF=BD=![]() ,∠DFC=∠CDF=45°
,∠DFC=∠CDF=45°
∴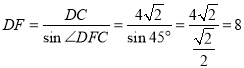
∴BC=DF,
∴∠A=∠
∴∠ADC=180°-45°-45°=90°,
∴∠ADF=90°-45°=45°=∠ABC
∴DF∥BC
∴四边形DFCB是平行四边形,
∴BF=2GF,DC=2CG
∴CG=![]()
在Rt△EFG中
![]()
∴BF=![]() ;
;
②如图,连接AF,取AB的中点T,连接GT
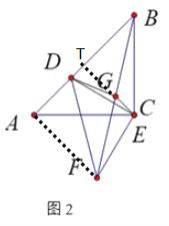
∵△ACB和△CDF是等腰直角三角形,
CA=CB,CD=CF,∠ACB=∠DCF=90°,∠CAB=45°,
∴∠ACF=∠BCD,
∴△ACF≌△BCD(SAS),
∴∠CAF=∠CBD=45°,AF=BD,
∴∠BAF=∠CAF+∠CAB=90°,
∴AF⊥AB,
∵AT=TB,BG=GF,
∴TG∥AF,
∴TG⊥AB,
∴点G的运动轨迹是Rt△ABC斜边的中线,运动的路径的长为![]() ;
;
(2)解:如图,当点G在直线EF上时,过点D作DJ⊥AC于点J,
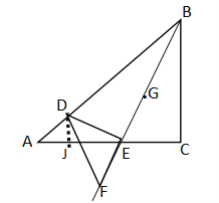
设AJ=DJ=x,则EJ=3-x,
∵∠DJE=∠C=∠DEB=90°,
∴∠DEJ+∠CEB=90°,∠CEB+∠CBE=90°,
∴∠DEJ=∠CEB
∴△DEJ∽△EBC
∴![]()
∴![]()
解之:![]()
∴![]()
∴![]() ;
;
当点G在直线DF上时,
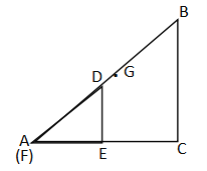
由题意得:![]()
当点G在直线DE上时,过点F作FT⊥CA交CA的延长线于点T,过点G作GK⊥AC于点K,过点D作DJ⊥AC于点J,
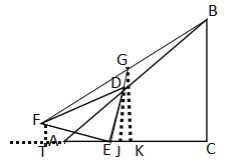
设FT=AT=y,
∵GK∥FT∥BC,GF=GB,
∴TK=KC,
∴![]()
∴![]()
∵∠T=∠GKE=∠FEG=90°,
易证∠FET=∠EGK
∴△FET∽△EGK
∴![]()
∴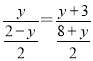
整理得:2y2+9y-6=0
解之:![]() (取正值),
(取正值),
∴![]()
易证△FET≌△EDJ,
∴![]()
![]()
当点G在直线DF上时,点D与点B重合,此时![]()
∴AD的长为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【点晴】
本题属于几何变换综合题,考查了等腰直角三角形的性质,平行四边形的判定和性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题,


科目:初中数学 来源: 题型:
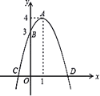
【题目】如图,已知抛物线的顶点为![]() ,抛物线与
,抛物线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.点
两点.点![]() 是抛物线上的一个动点.
是抛物线上的一个动点.
(1)求此抛物线的解析式;
(2)求![]() 、
、![]() 两点坐标及
两点坐标及![]() 的面积;
的面积;
(3)若点![]() 在
在![]() 轴下方的抛物线上.满足
轴下方的抛物线上.满足![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
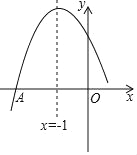
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=﹣1,与x轴的一个交点是A(﹣3,0)其图象的一部分如图所示,对于下列说法:①2a=b;②abc>0,③若点B(﹣2,y1),C(﹣![]() ,y2)是图象上两点,则y1<y2;④图象与x轴的另一个交点的坐标为(1,0).其中正确的是_____(把正确说法的序号都填上)
,y2)是图象上两点,则y1<y2;④图象与x轴的另一个交点的坐标为(1,0).其中正确的是_____(把正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投石机是古代的大型攻城武器,是数学、工程、物理等复杂学科相互融合的应用(如图(1)).在我国《元史·亦思马因传》中对这种投石机就有过记载(如图(2)).
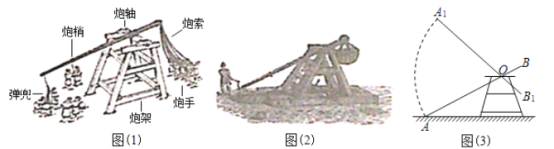
图(3)是图(1)中人工投石机的侧面示意图,炮架的横向支架均与地面相互平行,已知![]() 米,炮轴距地面4.5米,
米,炮轴距地面4.5米,![]()
![]() ,炮梢顶端点
,炮梢顶端点![]() 能到达水平地面,最高点能到达点
能到达水平地面,最高点能到达点![]() 处,且旋转的夹角
处,且旋转的夹角![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),求点
在同一平面内),求点![]() 到水平地面的距离.(参考数据:
到水平地面的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
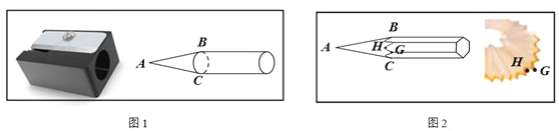
【题目】已知如图1,圆柱体铅笔插入卷笔刀充分卷削,得到底面直径BC为2的圆锥,∠BAC=30°.底面边长为1的正六棱柱铅笔插入卷削,得到如图2所示铅笔和锯齿状木屑(木屑厚度忽略不计),木屑锯齿齿锋点G相邻凹陷最低点为H,则AG=________,GH=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
| a |
| 12 |
| b |
| 10 |
学生立定跳远测试成绩的频数分布直方图
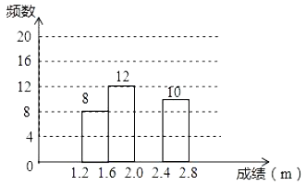
请根据图表中所提供的信息,完成下列问题:
(1)表中![]() ________,
________,![]() ________;
________;
(2)样本成绩的中位数落在________范围内;
(3)请把频数分布直方图补充完整;
(4)该校共有1200名学生,估计该学校学生立定跳远成绩在![]() 范围内的有多少人?
范围内的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com