
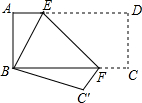
 如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度.
如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C'处,折痕为EF.如果∠ABE=20°,那么∠EFB=55度. 分析 由∠ABF、∠C′BF均与∠EBF互余可知∠C′BF=∠ABF=20°;由折叠特性可知∠BC′F=90°可得出∠BFC′=70°;再根据2∠EFB+∠BFC′=180°可得出结论.
解答 解:∵四边形ABCD为长方形,
∴∠ABC=∠D=∠C=90°.
由折叠的特性可知:∠BC′F=∠C=90°,∠EBC′=∠D=90°.
∵∠ABE+∠EBF=90°,∠C′BF+∠EBF=90°,且∠ABE=20°,
∴∠C′BF=20°.
∵∠BC′F=90°,
∴∠BFC′=90°-∠C′BF=70°.
又∵2∠EFB+∠BFC′=180°,
∴∠EFB=$\frac{180°-70°}{2}$=55°.
故答案为:55°.
点评 本题考查了长方形的性质以及折叠问题,解题的关键是找出∠BFC′的度数.本题属于基础题,难度不大,解决此类问题时,一定要注意到折叠时不变的量.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 2010 | 2011 | 2012 | 2013 | 2014 |
| 234 | 233 | 245 | 247 | 256 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
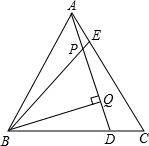 如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.
如图,在等边△ABC中,点D、E分别在边BC、AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com