
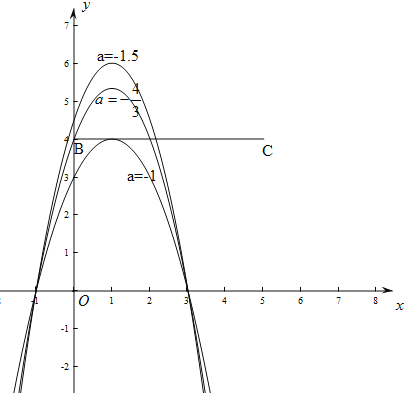
【题目】在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a (a<0)经过点A(-1,0),将点B(0,4)向右平移5个单位长度,得到点C.
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段BC恰有一个公共点,结合函数图像,求a的取值范围.
【答案】(1)C(5,4);(2)x=1; (3) ![]() 或
或![]()
【解析】
(1)根据坐标平移的特点是左减右加、上加下减可以求得点C的坐标;
(2)根据抛物线C1:y=ax2﹣2ax﹣3a(a≠0)可以求得该抛物线的对称轴;
(3)分三种情况讨论:①当抛物线顶点在线段BC上时,②当抛物线与直线BC的左交点在B的左边,右交点在线段BC上时,③当抛物线与直线BC的左交点在线段BC上,右交点在线段BC的延长线上时.
(1)∵点B(0,4)向右平移5个单位长度,得到点C,
∴点C的坐标为(5,4);
(2)∵抛物线C1:y=ax2﹣2ax﹣3a,
∴对称轴是直线x=﹣![]() =1;
=1;
(3)∵y=ax2﹣2ax﹣3a=a(x-1)2﹣4a,
∴分三种情况讨论:
①当抛物线顶点在线段BC上时,抛物线与线段BC只有一个交点,此时﹣4a=4,
解得:a=-1;
②当抛物线与直线BC的左交点在B的左边,右交点在线段BC上时,抛物线与线段BC只有一个交点,此时抛物线与y轴的交点在点B上方,
∴-3a>4,
解得:a<![]() .
.
③当抛物线与直线BC的左交点在线段BC上,右交点在线段BC的延长线上时,抛物线与线段BC只有一个交点.
∵抛物线开口向下,此时抛物线与x轴的右交点的横坐标一定大于5,这与抛物线一定过(-1,0)和(3,0)矛盾,此种情况不成立.
综上所述:a的取值范围是![]() 或a=-1.
或a=-1.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
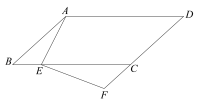
【题目】如图,在□ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
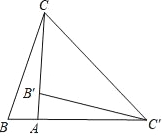
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 为正方形,已知点
为正方形,已知点![]() 、
、![]() ,点
,点![]() 、
、![]() 在第二象限内.
在第二象限内.
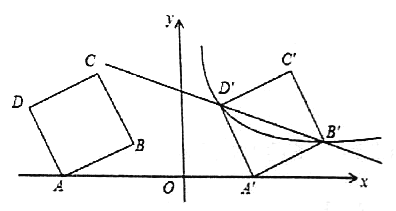
(1)点![]() 的坐标___________;
的坐标___________;
(2)将正方形![]() 以每秒
以每秒![]() 个单位的速度沿
个单位的速度沿![]() 轴向右平移
轴向右平移![]() 秒,若存在某一时刻
秒,若存在某一时刻![]() ,使在第一象限内点
,使在第一象限内点![]() 、
、![]() 两点的对应点
两点的对应点![]() 、
、![]() 正好落在某反比例函数的图象上,请求出此时
正好落在某反比例函数的图象上,请求出此时![]() 的值以及这个反比例函数的解析式;
的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在![]() 轴上的点
轴上的点![]() 和反比例函数图象上的点
和反比例函数图象上的点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点
四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
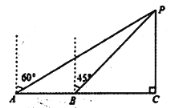
【题目】一艘货轮由西向东航行,在![]() 处测得灯塔
处测得灯塔![]() 在它的北偏东60°方向,继续航行到达
在它的北偏东60°方向,继续航行到达![]() 处,测得灯塔
处,测得灯塔![]() 在正南方向10海里的
在正南方向10海里的![]() 处是港口,点
处是港口,点![]() 、
、![]() 、
、![]() 在一条直线上,则这艘货轮由
在一条直线上,则这艘货轮由![]() 处到
处到![]() 处航行的路程为__________海里(结果保留根号).
处航行的路程为__________海里(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生对70周年国庆阅兵仪式直播的收看情况,某校对部分学生进行了一次调査,调査直播收看情况分三种:A.全程收看直播;B.观看了一部分直播;C.没有观看.学校学生会将调査数据进行了整理,并绘制了如下两幅不完整的统计图,请根据相关信息,解答下列问题:
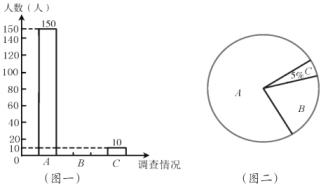
(1)本次活动共调查了______名学生;
(2)图二中![]() 区域的圆心角的度数为______;
区域的圆心角的度数为______;
(3)补全图;
(4)若该校学生共有3000名,请估计该校学生全程收看直播的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
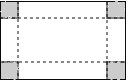
【题目】如图,有一块矩形硬纸板,长50cm,宽30cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为600cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
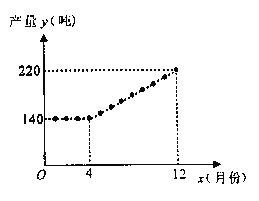
【题目】非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x(![]() ,且x为整数)之间的函数关系如图所示.
,且x为整数)之间的函数关系如图所示.
(1)请直接写出当![]() (x为整数)和
(x为整数)和![]() (x为整数)时,y与x的函数关系式;
(x为整数)时,y与x的函数关系式;
(2)若该饲养场生猪利润P(万元/吨)与月份x(![]() ,且x为整数)满足关系式:
,且x为整数)满足关系式:![]() ,请问:该饲养场哪个月的利润最大?最大利润是多少?
,请问:该饲养场哪个月的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com