
【题目】某工程,乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工程,已知甲工程队单独完成此工程所需天数是乙工程队单独完成此工程所需天数的 ![]() ,
,
(1)求:甲、乙工程队单独做完成此工程各需多少天?
(2)甲工程队每天的费用为0.67万元,乙工程队每天的费用为0.33万元,该工程的预算费用为20万元,若甲、乙工程队一起合作完成该工程,请问工程费用是否够用,若不够用应追加多少万元?
【答案】
(1)解:设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要 ![]() x天,则:
x天,则:
![]() +(
+( ![]() +
+ ![]() )×20=1,解得x=60.
)×20=1,解得x=60.
经检验:x=60是原方程的根,
![]() x=
x= ![]() ×60=40.
×60=40.
故甲队单独完成这项工程需要40天,乙队单独完成这项工程需要60天
(2)解:设甲、乙两队合作,完成这项工程需y天,则:
( ![]() +
+ ![]() )y=1,
)y=1,
解得y=24,
需要施工费用(0.67+0.33)×24=24(万元),
24﹣20=4(万元),
故工程费用不够用,应追加4万元
【解析】(1)可设乙工程队单独做完成此工程需x天,根据甲单独完成这项工程所需天数是乙单独完成这项工程所需天数的 ![]() 表示出甲工程队单独做完成此工程需
表示出甲工程队单独做完成此工程需 ![]() x天,再由乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工程,即可得出等量关系,进而求出即可;(2)求出甲、乙两队施工天数得出需要施工费用,即可分析得出.
x天,再由乙工程队单独先做10天后,再由甲、乙两个工程队合作20天就能完成全部工程,即可得出等量关系,进而求出即可;(2)求出甲、乙两队施工天数得出需要施工费用,即可分析得出.
【考点精析】解答此题的关键在于理解分式方程的应用的相关知识,掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点的位置如图所示,现将△ABC沿AA′的方向平移,使得点A移至图中的点A′的位置.
(1)在直角坐标系中,画出平移后所得△A′B′C′(其中B′、C′分别是B、C的对应点);
(2)求△ABC的面积;
(3)以A、B、C、D为顶点构造平行四边形,则D点坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.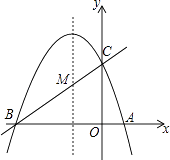
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数![]() 其中a、b、c不全相等且都不为
其中a、b、c不全相等且都不为![]() ,重新排列各数位上的数字可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为
,重新排列各数位上的数字可得到一个最大数和一个最小数,此最大数和最小数的差叫做原数的差数,记为![]() 例如,536的差数
例如,536的差数![]() .
.
(1)![]() ______,
______,![]() ______.
______.
(2)若一个三位数![]() 其中
其中![]() 且都不为
且都不为![]() ,求证:
,求证:![]() 能被99整除.
能被99整除.
(3)若s、t是各数位上的数字均不为0且互不相等两个三位自然数,s的个位数字为1,十位数字是个位数字的3倍,百位数字为x,t的百位数字为y,十位数字是百位数字的2倍,t的个位数字与s的百位数字相同![]() ,若
,若![]() 能被3整除,
能被3整除,![]() 能被11整除,求
能被11整除,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF , 其中正确的是( ) 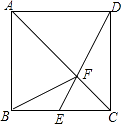
A.①③
B.②③
C.①④
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在春节来临之际,小杨的服装小店用2500元购进了一批时尚围巾,上市后很快售完,小杨又用8400元购进第二批这种围巾,所购数量是第一批购进数量的3倍,但每条围巾的进价多了3元.
(1)小杨两次共购进这种围巾多少条?
(2)如果这两批围巾每条的售价相同,且全部售完后总利润率不低于20%,那么每条围巾的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在安庆市第三届中小学生道路交通安全网络知识竞赛活动中,某中学的老师要求同学们都参加社会实践活动,一天,王明和张强两位同学到市中心的广场的十字路口,观察、统计上午7:![]() :00中闯红灯的人次,制作了如下的两个数据统计图
:00中闯红灯的人次,制作了如下的两个数据统计图![]() 井且提出了一些问题
井且提出了一些问题
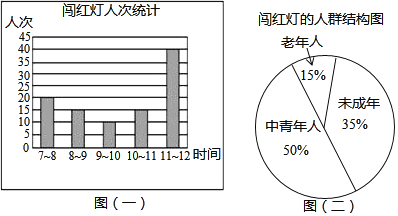
![]() 求图
求图![]() 一
一![]() 提供的五个数据
提供的五个数据![]() 各时段闯红灯人次
各时段闯红灯人次![]() 的平均数
的平均数![]() 并说明这两幅统计图各有什么特点?
并说明这两幅统计图各有什么特点?
![]() 估计一个月
估计一个月![]() 按30天计算
按30天计算![]() 上午7:
上午7:![]() :00在该十字路口闯红灯的未成年人约有多少人次?
:00在该十字路口闯红灯的未成年人约有多少人次?
![]() 请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
请你根据统计图提供的信息向交通管理部门提出一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com