
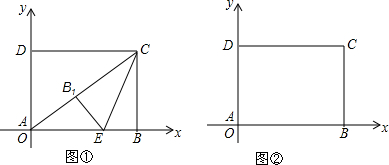
分析 (1)根据四边形ABCD是矩形,于是得到CD=AB=8,BC=AD=6,∠ADC=∠CBA=90°,即可求得C(8,6);
(2)在Rt△ABC中,根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,根据折叠的性质得到CB1=6,B1E=BE,∠CB1E=∠EBC=90°,于是得到AB1=4,∠AB1E=90°,根据勾股定理列方程即可得到结论;
(3)如图②,若△PAB为等腰三角形:①当PA=PB,即点P在AB的垂直平分线上,于是得到P(4,6);②当AB=AP=8,根据勾股定理得到DP=$\sqrt{A{P}^{2}-A{D}^{2}}$=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$,求得P(2$\sqrt{7}$,6);③当BA=BP=8,根据勾股定理得到即CP2+62=82求得P(8-2$\sqrt{7}$,0).
解答 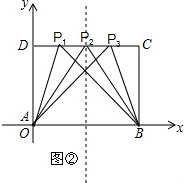 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,
∴CD=AB=8,BC=AD=6,∠ADC=∠CBA=90°,
∴C(8,6);
(2)在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵折叠△CEB使B落在线段AC的B处,
∴△BCE≌△B1CE,
∴CB1=6,B1E=BE,∠CB1E=∠EBC=90°,
∴AB1=4,∠AB1E=90°,
∴AE2=AB12+B1E2,
即AE2=42+(8-AE)2,
解得:AE=5,∴E(5,0);
(3)如图②,若△PAB为等腰三角形,
①当PA=PB,即点P在AB的垂直平分线上,
∴P(4,6);
②当AB=AP=8,
∴DP=$\sqrt{A{P}^{2}-A{D}^{2}}$=$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$,
∴P(2$\sqrt{7}$,6);
③当BA=BP=8,CP2+BC2=BP2,即CP2+62=82,
∴PC=2$\sqrt{7}$,
∴DP=8-2$\sqrt{7}$,
∴P(8-2$\sqrt{7}$,0);
综上所述:若△PAB为等腰三角形,P点坐标为:(8-2$\sqrt{7}$,0),(4,0)(2$\sqrt{7}$,0).
点评 本题考查了矩形的性质,折叠的性质,勾股定理,等腰三角形的判定和性质,求点的坐标,注意(3)要分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
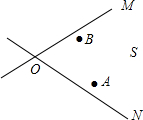 如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)
如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
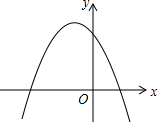 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个同号的实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
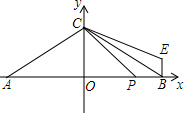 已知如图,A(-4,0)、C(0,4),点B在x轴正半轴上,AC=BC,D点坐标为(3,0),连接CD,将△BCD沿直线BC折,E点为D点的对应点.
已知如图,A(-4,0)、C(0,4),点B在x轴正半轴上,AC=BC,D点坐标为(3,0),连接CD,将△BCD沿直线BC折,E点为D点的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com