
【题目】已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC=3∠ACD.

(1)如图1,求证:AB=AC;
(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;
(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:![]() ,CF=12,连接PF,求PF的长.
,CF=12,连接PF,求PF的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接AD.设∠BEC=3α,∠ACD=α,利用等量代换得出∠ABC=∠ACB,最后进一步证明结论即可;
(2)连接AD,在CD上取一点Z,使得CZ=BD,通过证明△ADB≌△AZC得出AD=AZ,然后进一步证明即可;
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T,利用三角函数以及勾股定理进一步求解即可.
(1)证明:如图1中,连接AD.设∠BEC=3α,∠ACD=α.
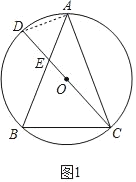
∵∠BEC=∠BAC+∠ACD,
∴∠BAC=2α,
∵CD是直径,
∴∠DAC=90°,
∴∠D=90°﹣α,
∴∠B=∠D=90°﹣α,
∵∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣2α﹣(90°﹣α)=90°﹣α.
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:如图2中,连接AD,在CD上取一点Z,使得CZ=BD.
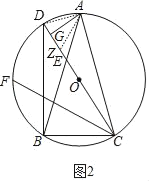
∵弧BD=弧CF,
∴DB=CF,
∵∠DBA=∠DCA,CZ=BD,AB=AC,
∴△ADB≌△AZC(SAS),
∴AD=AZ,
∵AG⊥DZ,
∴DG=GZ,
∴CG=CZ+GZ=BD+DG=CF+DG.
(3)连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.
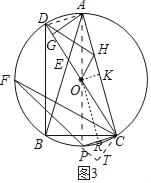
∵CP⊥AC,
∴∠ACP=90°,
∴PA是直径,
∵OR⊥PC,OK⊥AC,
∴PR=RC,∠ORC=∠OKC=∠ACP=90°,
∴四边形OKCR是矩形,
∴RC=OK,
∵OH:PC=1:![]() ,
,
∴设OH=![]() a,PC=2a,
a,PC=2a,
∴PR=RC=a,
∴RC=OK=a,sin∠OHK=![]() ,
,
∴∠OHK=45°,
∵OH⊥DH,
∴∠DHO=90°,
∴∠DHA=180°﹣90°﹣45°=45°,
∵CD是直径,
∴∠DAC=90°,
∴∠ADH=90°﹣45°=45°,
∴∠DHA=∠ADH,
∴AD=AH,
∵∠COP=∠AOD,
∴AD=PC,
∴AH=AD=PC=2a,
∴AK=AH+HK=2a+a=3a,
在Rt△AOK中,tan∠OAK=![]() ,OA=
,OA=![]() =
=![]() ,
,
∴sin∠OAK=![]() ,
,
∵∠ADG+∠DAG=90°,∠ACD+∠ADG=90°,
∴∠DAG=∠ACD,
∵AO=CO,
∴∠OAK=∠ACO,
∴∠DAG=∠ACO=∠OAK,
∴tan∠ACD=tan∠DAG=tan∠OAK=![]() ,
,
∴AG=3DG,CG=3AG,
∴CG=9DG,
由(2)可知,CG=DG+CF,
∴DG+12=9DG,
∴DG=![]() ,AG=3DG=3×
,AG=3DG=3×![]() =
=![]() ,
,
∴AD=![]() ,
,
∴PC=AD=![]() ,
,
∵sin∠F=sin∠OAK,
∴sin∠F=![]() ,
,
∴CT=![]() =
=![]() ×12=
×12=![]() ,FT=
,FT=![]() ,PT=
,PT=![]() ,
,
∴PF=FT﹣PT=![]() ﹣
﹣![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象如图所示,与
的图象如图所示,与![]() 轴的交点分别
轴的交点分别![]() ,且函数与
,且函数与![]() 轴交点在
轴交点在![]() 的下方,现给以下结论:①
的下方,现给以下结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;④
;④![]() .则下列说法正确的是( )
.则下列说法正确的是( )

A.①②B.①③C.①④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
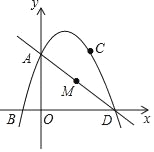
【题目】如图,抛物线y=ax2+bx+3经过点 B(﹣1,0),C(2,3),抛物线与y轴的焦点A,与x轴的另一个焦点为D,点M为线段AD上的一动点,设点M的横坐标为t.
(1)求抛物线的表达式;
(2)过点M作y轴的平行线,交抛物线于点P,设线段PM的长为1,当t为何值时,1的长最大,并求最大值;(先根据题目画图,再计算)
(3)在(2)的条件下,当t为何值时,△PAD的面积最大?并求最大值;
(4)在(2)的条件下,是否存在点P,使△PAD为直角三角形?若存在,直接写出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
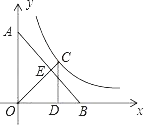
【题目】如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=![]() (x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=_____.
(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程y(米)与时间x(分)的函数关系如图2所示.
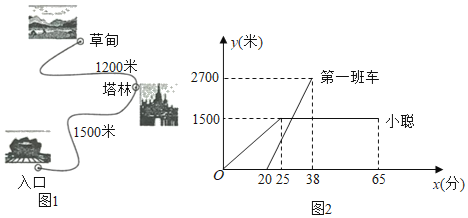
(1)求第一班车离入口处的路程y(米)与时间x(分)函数表达式.并写出x的取值范围;
(2)求第一班车从入口处到达塔林所需的时间;
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年伊始,一场突如其来的疫情防控战在中华大地骤然打响,全国人民自觉居家减少外出,师生停课不停学,举国共抗疫情.某中学在复学后,为了了解学生们在居家期间的生活状态,以更好地保护复学后学生们的身心健康,对本校学生进行了“居家期间学习之余主要活动”的抽样调查.种类为:(A)强身健体、(B)艺术熏陶、(C)经典阅读、(D)分担劳动、(E)其他.针对以上活动种类,统计学生们花时间最多的种类的人数,以绘制成如下两幅不完整的条形统计图和扇形统计图.
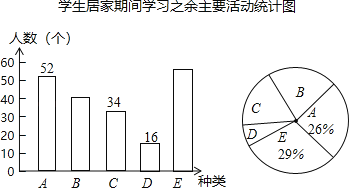
请根据图中的信息,回答下列问题.
(1)被抽样调查的总人数为 人;
(2)补全条形统计图;
(3)若该校共有学生1800人,请估算种类D的大约人数;
(4)据此疫情经历,给自己提出一条人生建议 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.



A:踢毽子 B:乒乓球 C:篮球 D:跳绳
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,求表示区域D的扇形圆心角的度数;
(3)全校学生中喜欢篮球的人数大约是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
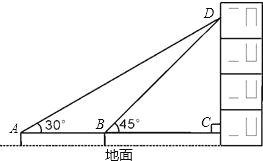
【题目】在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处,测得条幅顶端D的仰角为30°,再向条幅方向前进10米后,又在点B处测得条幅顶端D的仰角为45°,已知测点A、B和C离地面高度都为1.44米,求条幅顶端D点距离地面的高度.(计算结果精确到0.1米,参考数据:![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com