
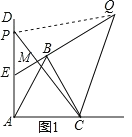
【题目】如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连接QB并延长交直线AD于E.

(1)如图1,猜想∠QEP= ;
(2)如图2,若当∠DAC是锐角时,其他条件不变,猜想∠QEP的度数,并证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=6,求BQ的长.
【答案】(1)60°;(2)∠QEP=60°.证明见解析;(3)BQ=3![]() ﹣3
﹣3![]() .
.
【解析】
(1)如图1,先根据旋转的性质和等边三角形的性质得出∠PCA=∠QCB,进而可利用SAS证明△CQB≌△CPA,进而得∠CQB=∠CPA,再在△PEM和△CQM中利用三角形的内角和定理即可求得∠QEP=∠QCP,从而完成猜想;
(2)以∠DAC是锐角为例,如图2,仿(1)的证明思路利用SAS证明△ACP≌△BCQ,可得∠APC=∠Q,进一步即可证得结论;
(3)仿(2)可证明△ACP≌△BCQ,于是AP=BQ,再求出AP的长即可,作CH⊥AD于H,如图3,易证∠APC=30°,△ACH为等腰直角三角形,由AC=4可求得CH、PH的长,于是AP可得,问题即得解决.
解:(1)∠QEP=60°;
证明:连接PQ,如图1,由题意得:PC=CQ,且∠PCQ=60°,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠PCA=∠QCB,
则在△CPA和△CQB中,
 ,
,
∴△CQB≌△CPA(SAS),
∴∠CQB=∠CPA,
又因为△PEM和△CQM中,∠EMP=∠CMQ,
∴∠QEP=∠QCP=60°.
故答案为:60°;
(2)∠QEP=60°.
证明:如图2,∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°,
∵线段CP绕点C顺时针旋转60°得到线段CQ,
∴CP=CQ,∠PCQ=60°,
∴∠ACB+∠BCP=∠BCP+∠PCQ,
即∠ACP=∠BCQ,
在△ACP和△BCQ中,
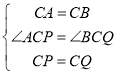 ,
,
∴△ACP≌△BCQ(SAS),
∴∠APC=∠Q,
∵∠1=∠2,
∴∠QEP=∠PCQ=60°;
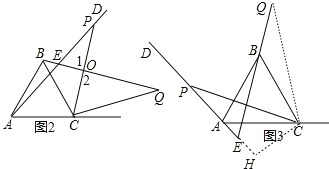
(3)连结CQ,作CH⊥AD于H,如图3,
与(2)一样可证明△ACP≌△BCQ,
∴AP=BQ,
∵∠DAC=135°,∠ACP=15°,
∴∠APC=30°,∠CAH=45°,
∴△ACH为等腰直角三角形,
∴AH=CH=![]() AC=
AC=![]() ×4=
×4=![]() ,
,
在Rt△PHC中,PH=![]() CH=
CH=![]() ,
,
∴PA=PHAH=![]() -
-![]() ,
,
∴BQ=![]() -
-![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
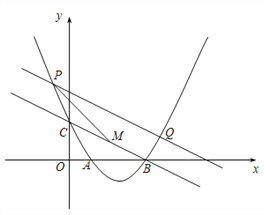
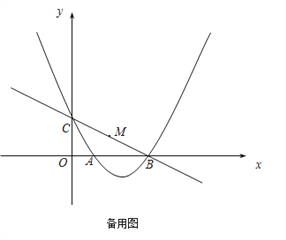
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点P为抛物线上一动点,过点P作PQ∥BC交抛物线于点Q,P、Q两点之间的距离为m.
与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点P为抛物线上一动点,过点P作PQ∥BC交抛物线于点Q,P、Q两点之间的距离为m.
(1)求直线BC的解析式;
(2)取线段BC的中点M,连接PM.当m最小时,判断以点P、O、M、B为顶点的四边形是什么特殊的平行四边形,并说明理由;
(3)设N为y轴上一点,在(2)的基础上,当∠OBN=2∠OBP时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

(1)根据上表填空:
①抛物线与x轴的交点坐标是______和______;
②抛物线经过点(-3,______);
(2)试确定抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如表数据:
轿车行驶的路程s(km) | 0 | 100 | 200 | 300 | 400 | … |
油箱剩余油量Q(L) | 50 | 42 | 34 | 26 | 18 | … |
(1)该轿车油箱的容量为______L,行驶150km时,油箱剩余油量为______L;
(2)根据上表的数据,写出油箱剩余油量Q(L)与轿车行驶的路程s(km)之间的表达式;
(3)某人将油箱加满后,驾驶该轿车从A地前往B地,到达B地时邮箱剩余油量为26L,求A,B两地之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°.
(1)用尺规作图作Rt△ABC的重心P.(保留作图痕迹,不要求写作法和证明);
(2)你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心之间的距离?并请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校美术组要购买铅笔和橡皮,按照商店规定,若同时购买60支铅笔和30块橡皮,则需按零售价购买,共需支付30元;若同时购买90支铅笔和60块橡皮,则可按批发价购买,共需支付40.5元.已知每支铅笔的批发价比零售价低0.05元,每块橡皮的批发价比零售价低0.10元.求每支铅笔和每块橡皮的批发价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,M是BC边上的点(不与B,C两点重合),AB=AM,点B关于直线AM对称的点是N,连接DN,设∠ABC,∠CDN的度数分别为![]() ,
,![]() ,则
,则![]() 关于
关于![]() 的函数解析式是_______________________________.
的函数解析式是_______________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com