练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

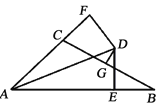
    【题目】如图，∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E，F，AB=11，AC=5，则BE=______________．

    【答案】3

    【解析】如图，连接CD，BD，已知AD是∠BAC的平分线，DE⊥AB，DF⊥AC，根据角平分线的性质可得DF=DE，∠F=∠DEB=90°，∠ADF=∠ADE，即可得AE=AF，又因DG是BC的垂直平分线，所以CD=BD，在Rt△CDF和Rt△BDE中，CD＝BD，DF＝DE，利用HL定理可判定Rt△CDF≌Rt△BDE，由全等三角形的性质可得BE=CF，所以AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE，又因AB=11，AC=5，所以BE=3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，为了改造小区环境，某小区决定要在一块一边靠墙（墙的最大可使用长度13 m）的空地上建造一个矩形绿化带．除靠墙一边（AD）外，用长为36 m的栅栏围成矩形ABCD，中间隔有一道栅栏（EF）．设绿化带宽AB为x m，面积为S m2

    （1） 求S与x的函数关系式，并求出x的取值范围

    （2） 绿化带的面积能达到108 m2吗？若能，请求出AB的长度；若不能，请说明理由

    （3） 当x为何值时，满足条件的绿化带面积最大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某科研小组在网上获取了声音在空气中传播的速度y与空气温度x关系的一些数据（如下表）：

    下列说法错误的是（　 ）

    A.在这个变化中，自变量是温度，因变量是声速B.温度越高，声速越快

    C.当空气温度为20℃时，声音5s可以传播1740mD.温度每升高10℃，声速提高6m/s.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠DAC＝90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连接CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连接QB并延长交直线AD于E．

    （1）如图1，猜想∠QEP＝　 　；

    （2）如图2，若当∠DAC是锐角时，其他条件不变，猜想∠QEP的度数，并证明；

    （3）如图3，若∠DAC＝135°，∠ACP＝15°，且AC＝6，求BQ的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在ABCD中，E是AD上一点，AE=AB，过点E作直线EF，在EF上取一点G，使得∠EGB=∠EAB，连接AG．

    （1）如图1，当EF与AB相交时，若∠EAB=60°，求证：EG=AG+BG；

    （2）如图2，当EF与AB相交时，若∠EAB=α（0°＜α＜90°），请你直接写出线段EG、AG、BG之间的数量关系（用含α的式子表示）；

    （3）如图3，当EF与CD相交时，且∠EAB=90°，请你写出线段EG、AG、BG之间的数量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的袋中装有3个绿球，5个红球和若干白球，它们除颜色外其他都相同，将球搅匀，从中任意摸出一个球．

    （1）若袋内有4个白球，从中任意摸出一个球，是绿球的概率为　 　，是红球的概率为　 　，是白球的概率为　 　．

    （2）如果任意摸出一个球是绿球的概率是，求袋中有几个白球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知⊙O的半径为1，PQ是⊙O的直径，n个相同的正三角形沿PQ排成一列，所有正三角形都关于PQ对称，其中第一个△A1B1C1的顶点A1与点P重合，第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn，Cn在圆上.

    (1)如图②，当n＝1时，求正三角形的边长a1.

    (2)如图③，当n＝2时，求正三角形的边长a2.

    (3)如图①，求正三角形的边长an(用含n的代数式表示).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面的统计图反映了我国2013年到2017年国内生产总值情况.（以上数据摘自国家统计局《中华人民共和国2017年国民经济和社会发展统计公报》，其中国内生产总值绝对数按现价计算，增长速度按不变价格计算）

    根据统计图提供的信息，下列推断合理的是

    A.从2013-2017年，我国国内生产总值逐年下降

    B.从2013-2017年，我国国内生产总值的增长率逐年下降

    C.从2013-2017年，我国国内生产总值的平均增长率约为6.7%

    D.计算同上年相比的增量，2017年我国国内生产总值的增量为近几年最多

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线（且）与轴交于点，过点作直线轴，且与交于点.

    （1）当，时，求的长；

    （2）若，，且轴，判断四边形的形状，并说明理由.

    查看答案和解析>>

    同步练习册答案