
【题目】如图所示,为了改造小区环境,某小区决定要在一块一边靠墙(墙的最大可使用长度13 m)的空地上建造一个矩形绿化带.除靠墙一边(AD)外,用长为36 m的栅栏围成矩形ABCD,中间隔有一道栅栏(EF).设绿化带宽AB为x m,面积为S m2
(1) 求S与x的函数关系式,并求出x的取值范围
(2) 绿化带的面积能达到108 m2吗?若能,请求出AB的长度;若不能,请说明理由
(3) 当x为何值时,满足条件的绿化带面积最大

【答案】(1)S=-3x2+36x(![]() ≤x<12)(2)不能 (3)
≤x<12)(2)不能 (3)![]()
【解析】试题分析:(1)首先根据矩形的性质,由绿化带的AB边长为x(m),可得BC=36-3x ,然后根据矩形面积的求解方法,即可求得y与x之间的函数关系式,又由墙的最大可使用长度13 m,即可求得自变量的x的范围.
(2)令y=108解方程后判断即可;
(3)根据(1)中的二次函数的增减性,可知当x>6时,y随x的增大而减小,故可得当x=![]() 时,y最大,从而得到结论.
时,y最大,从而得到结论.
试题解析:解:(1)∵四边形ABCD是矩形,∴AB=CD=EF,AD=BC,∵AB=xm,AB+BC+CD+EF=36m,∴BC=36-3x,∴绿化带的面积为:y=x(36-3x)=﹣3x2+36x,由![]() ,解得:
,解得: ![]() ,∴y与x之间的函数关系式为:y=﹣3x2+36x(
,∴y与x之间的函数关系式为:y=﹣3x2+36x(![]() );
);
(2)由题意得:﹣3x2+36x=108,解得:x1=x2=6,∵6<![]() ,∴绿化带的面积不能达到108 m2.
,∴绿化带的面积不能达到108 m2.
(3)∵y=﹣3x2+36x =﹣3(x﹣6)2+108,∵a=﹣3<0,∴当x>6时,y随x的增大而减小,∴当x=![]() 时,y最大,∴当x取
时,y最大,∴当x取![]() 时绿化带的面积最大.
时绿化带的面积最大.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】某校准备组织七年级400名学生参加北京夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人;用1辆小客车和2辆大客车每次可运送学生110人;
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满;
①请你设计出所有的租车方案;
②若小客车每辆需租金4000元,大客车每辆需租金7600元,请选出最省钱的租车方案,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
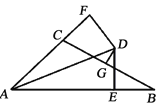
【题目】如图,AE=AC,AB=AD,∠EAB=∠CAD.
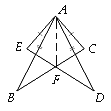
(1)BC与DE相等吗?说明理由.
(2)若BC与DE相交于点F,EF=CF.连接AF,∠BAF与∠DAF相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
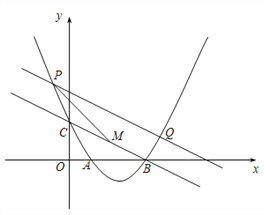
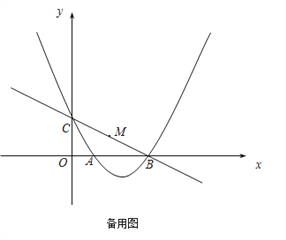
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点P为抛物线上一动点,过点P作PQ∥BC交抛物线于点Q,P、Q两点之间的距离为m.
与x轴交于A,B两点(点A在点B的左边),与y轴交于点C.点P为抛物线上一动点,过点P作PQ∥BC交抛物线于点Q,P、Q两点之间的距离为m.
(1)求直线BC的解析式;
(2)取线段BC的中点M,连接PM.当m最小时,判断以点P、O、M、B为顶点的四边形是什么特殊的平行四边形,并说明理由;
(3)设N为y轴上一点,在(2)的基础上,当∠OBN=2∠OBP时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于M,AE⊥BD于E,交CD于N,连AC
(1)求证:AC=AN;
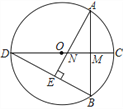
(2)若OM∶OC=3∶5,AB=5,求⊙O的半径;
查看答案和解析>>
科目:初中数学 来源: 题型:
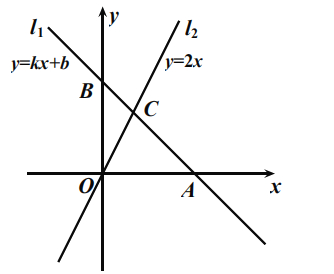
【题目】如图,直线l1:y=kx+b(k≠0)与x轴交于点A(3,O),与y轴交于点B(0,3), 直线l 2:y=2x与直线l1相交于点C.
(1)求直线 l1 的解析式;
(2)求点C的坐标和△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期数学家刘徽编撰的最早一部测量数学著作《海岛算经》中有一题:今有望海岛,立两表齐高三丈,前后相去千步,令后表与前表参相直.从前表却行一百二十三步,人目着地,取望岛峰,与表末参合.从后表却行一百二十七步,人目着地,取望岛峰,亦与表末参合.问岛高几何?

译文:今要测量海岛上一座山峰AH的高度,在B处和D处树立标杆BC和DE,标杆的高都是3丈,B和D两处相隔1000步(1丈=10尺,1步=6尺),并且AH,CB和DE在同一平面内.从标杆BC后退123步的F处可以看到顶峰A和标杆顶端C在同一直线上;从标杆ED后退127步的G处可以看到顶峰A和标杆顶端E在同一直线上.则山峰AH的高度是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

(1)根据上表填空:
①抛物线与x轴的交点坐标是______和______;
②抛物线经过点(-3,______);
(2)试确定抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com