Question

四边形ABCD为矩形，G是BC上的任意一点，DE⊥AG于点E．

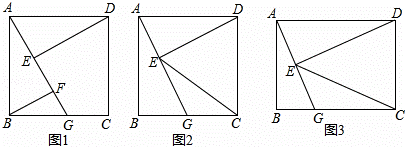
（1）如图1，若AB=BC，BF∥DE，且交AG于点F，求证：AF﹣BF=EF；

（2）如图2，在（1）条件下，AG=BG，求；

（3）如图3，连EC，若CG=CD，DE=2，GE=1，则CE=　_________　（直接写出结果）

Answer 1

　

考点：	四边形综合题．
分析：	（1）利用△AED≌△BFA求得AE=BF，再利用线段关系求出AF﹣BF=EF． （2）延长AG与DC交于点F，设BG=t先求出AB，再利用△ABG≌△FCG及直角三角形斜边上的中点，求出； （3）连接DG，作EM⊥BC于M点，利用直角三角形求出DG，CD的长，再利用ABG∽△DEA，求出AD，再运用△EMG∽△DEA求出EM和MG，再运用勾股定理即可求出CE的长．
解答：	（1）证明：∵四边形ABCD为矩形，AB=BC， ∴四边形ABCD为正方形， ∴AD=AB，∠BAD=90°， 又DE⊥AG，BF∥DE， ∴∠AED=∠AFB=90°， ∵∠BAF+∠DAE=90°，∠BAE+∠ABF=90°， ∴∠DAE=∠ABF， 在△AED和△BFA中， ∴△AED≌△BFA（AAS）， ∴AE=BF， ∴AF﹣BF=EF， （2）如图2，延长AG与DC交于点F， ∵AG=BG，设BG=t，则AG=t， 在Rt△ABG中，AB==2t， ∴G为BC的中点， 在△ABG和△FCG中， ∴△ABG≌△FCG（AAS）， ∴AB=FC=CD， 又∵DE⊥AG， 在Rt△DEF中，C为斜边DF的中点， ∴EC=CD=CF， ∴== （3）如图3，连接DG，作EM⊥BC于M点， ∵DE⊥AG，DE=2，GE=1， ∴在RT△DEG中，DG===， ∵CG=CD， ∴在RT△DCG中，∠CDG=∠CGD=45°， ∴CD=CG==， ∵∠BAG+∠GAD=90°，∠EDA+∠GAD=90°， ∴∠BAG=∠EDA， ∵∠ABG=∠DEA=90°， ∴△ABG∽△DEA， ∴=， 设AD=x，则AE==，AG=+1， ∴=， 解得x1=，x2=﹣2（舍去） ∴AE==， 又∵∠BAG=∠MEG， ∴∠EDA=∠MEG， ∴△EMG∽△DEA ∴==，即== 解得EM=，MG=， ∴CM=CG+MG=+=， ∴CE===． 故答案为：．
点评：	本题主要考查了四边形综合题，解题的关键是正确作出辅助线，运用三角形相似求出线段的长度．此题难度较大，考查了学生计算能力．解题是一定要细心．