
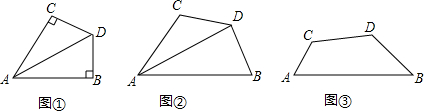
分析 探究:证明△DFC≌△DEB即可.
应用:先证明△DFC≌△DEB,再证明△ADF≌△ADE,结合BE=$\frac{1}{2}$BD即可解决问题.
解答 探究:证明:如图②中,DE⊥AB于E,DF⊥AC于F,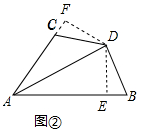
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中$\left\{\begin{array}{l}{∠F=∠DEB}&{\;}\\{∠FCD=∠B}&{\;}\\{DF=DE}&{\;}\end{array}\right.$,
∴△DFC≌△DEB(AAS),
∴DC=DB.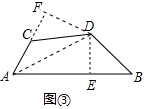
应用:解:如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,$\left\{\begin{array}{l}{∠F=∠DEB}&{\;}\\{∠FCD=∠B}&{\;}\\{DC=DB}&{\;}\end{array}\right.$,
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴△RtADF≌Rt△ADE(HL),
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE,
在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=60°,BD=a,
∴∠BDE=30°,
∴BE=$\frac{1}{2}$BD=$\frac{1}{2}$a
∴AB-AC=2BE=a.
点评 本题是三角形综合题目,考查了全等三角形的判定和性质、角平分线的性质、等腰直角三角形的性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
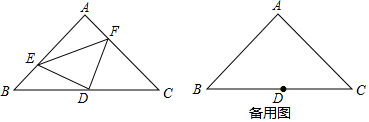
 (1)根据作图要求(尺规作图,保留作图痕迹,不写作法).
(1)根据作图要求(尺规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
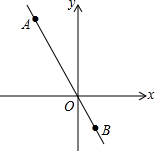 已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求:
已知正比例函数y=kx(k≠0)的图象经过A(-2,4),B(1,b).求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
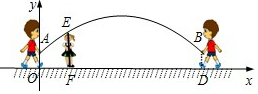 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
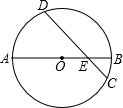 如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求
如图,⊙O的直径AB与弦CD交于点E,AE=5,BE=1,CD=4$\sqrt{2}$,求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com