
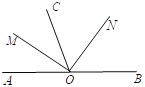
【题目】如图,O为直线AB上一点,OM是∠AOC的角平分线,ON是∠COB的平分线
(1)指出图中所有互为补角的角,
(2)求∠MON的度数,
(3)指出图中所有互为余角的角.
【答案】(1)∠AOM与∠MOB,∠AOC与∠BOC,∠AON与∠BON,∠COM与∠MOB,∠CON与∠AON;(2)90![]() ;(3)∠AOM与∠BON,∠COM与∠BON,∠CON与∠AOM,∠CON与∠COM
;(3)∠AOM与∠BON,∠COM与∠BON,∠CON与∠AOM,∠CON与∠COM
【解析】
(1)根据补角的定义:如果两个角的和为180°,则这两个角互为补角,观察图形,根据∠AOB=180°,即可解答.
(2)根据OM是∠AOC的角平分线,ON是∠COB的平分线,可得∠AOM=∠MOC,∠CON= NOB,此时结合∠AOB的度数即可得到∠MON的度数.
(3)根据余角的定义:如果两个角的和为90°,则这两个角互为余角,结合∠MON的度数,分析图形,即可解答.
(1)∵∠AOB=180°
∴∠AOM+∠BOM=180°,∠AOC+∠BOC=180°,∠AON+∠BON=180,
又∵OM是∠AOC的角平分线,ON是∠COB的平分线,
∴∠AOM=∠MOC,∠CON= NOB,
∴∠COM+∠MOB=180°,∠CON+∠AON=180°.
故图中所有互为补角的角有:∠AOM与∠MOB,∠AOC与∠BOC,∠AON与∠BON,∠COM与∠MOB,∠CON与∠AON.
(2)∵OM是∠AOC的角平分线,ON是∠COB的平分线,
∴∠MOC=![]() ∠AOC,∠CON=
∠AOC,∠CON=![]() ∠COB,
∠COB,
∴MON=∠MOC+∠CON=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB,
∠AOB,
又∵∠AOB=180°,
∴MON=90°.
(3)∵OM是∠AOC的角平分线,ON是∠COB的平分线,
∴∠AOM=∠MOC,∠CON= NOB,
又∵MON=90°,
∴∠AOM+∠BON=90°,∠COM+∠BON=90°,∠CON+∠AOM=90°,∠CON+∠COM=90°
故图中所有互为余角的角有:∠AOM与∠BON,∠COM与∠BON,∠CON与∠AOM,∠CON与∠COM.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
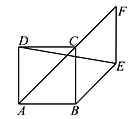
【题目】如图,四边形ABCD是正方形,AB=1,点F是对角线AC延长线上一点,以BC、CF为邻边作菱形BEFC,连接DE,则DE的长是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
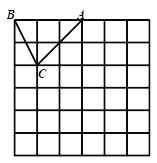
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
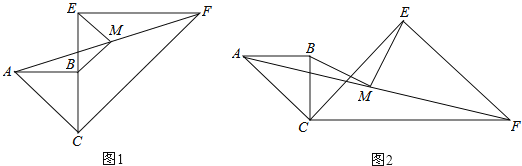
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一张矩形纸片的长AD=12,宽AB=2,点E在边AD上,点F在边BC上,将四边形ABFE沿直线EF翻折后,点B落在边AD的三等分点G处,则EG的长为_______.
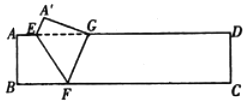
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一块四边形的木板余料ABCD,经测量AB=25cm,BC=54cm,CD=30cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面积为____________.
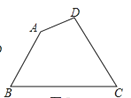
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
的图象在第一象限交于点A(4,2),与y轴的负半轴交于点B,且OB=6.
(1)求函数y=![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)已知直线AB与x轴相交于点C,在第一象限内,求反比例函数y=![]() 的图象上一点P,使得S△POC=9.
的图象上一点P,使得S△POC=9.
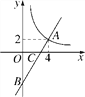
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
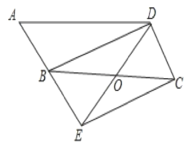
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD=___°时,四边形BECD是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com