练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，AB=13cm，AC=20cm，BC边上的高为12cm，则△ABC的面积为cm2 ．

    【答案】126或66
    【解析】解：当∠B为锐角时（如图1），
    在Rt△ABD中，
    BD= = =5cm，
    在Rt△ADC中，
    CD= = =16cm，
    ∴BC=21，
    ∴S△ABC= = ×21×12=126cm2；
    当∠B为钝角时（如图2），

    在Rt△ABD中，
    BD= = =5cm，
    在Rt△ADC中，
    CD= = =16cm，
    ∴BC=CD﹣BD=16﹣5=11cm，
    ∴S△ABC= = ×11×12=66cm2 ，
    故答案为：126或66．
    此题分两种情况：∠B为锐角或∠B为钝角已知AB、AC的值，利用勾股定理即可求出BC的长，利用三角形的面积公式得结果．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下表

    我们把某格中字母和所得的多项式称为特征多项式，例如第1格的“特征多项式”为4x＋y，回答下列问题：

    （1）第3格的“特征多项式”为 ，第4格的“特征多项式”为 ，第n格的“特征多项式”为 ；

    （2）若第1格的“特征多项式”的值为－10，第2格的“特征多项式”的值为－16，求x，y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O的半径是6，点O到直线l的距离为5，则直线l与⊙O的位置关系是（ ）
    A.相离
    B.相切
    C.相交
    D.无法判断

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC和△DBE均为等腰直角三角形．
    （1）求证：AD=CE；
    （2）求证：AD和CE垂直．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F．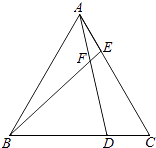
    （1）求证：△ABE≌△CAD；
    （2）求∠BFD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于函数y=﹣2x+1，下列结论正确的是( )

    A. 图象经过点（﹣2，1） B. y随x的增大而增大

    C. 图象不经过第三象限 D. 图象不经过第二象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：四边形ABCD中，AB=CB= ，CD= ，DA=1，且AB⊥CB于B．

    试求：
    （1）∠BAD的度数；
    （2）四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在三角形ABC中，∠A=80°，OB、OC分别平分∠ABC和∠ACB，你能求出∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题提出】

    如图①，已知△ABC是等腰三角形，点E在线段AB上，点D在直线BC上，且ED=EC，将△BCE绕点C顺时针旋转60°至△ACF连接EF．试证明：AB=DB+AF；

    【类比探究】

    （1）如图②，如果点E在线段AB的延长线上，其他条件不变，线段AB，DB，AF之间又有怎样的数量关系？请说明理由；

    （2）如果点E在线段BA的延长线上，其他条件不变，请在图③的基础上将图形补充完整，并写出AB，DB，AF之间的数量关系，不必说明理由．

    查看答案和解析>>

    同步练习册答案