
����Ŀ�������������
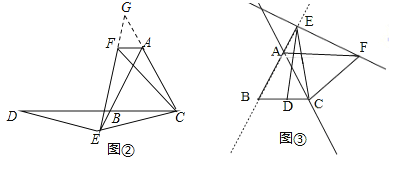
��ͼ�٣���֪��ABC�ǵ��������Σ���E���߶�AB�ϣ���D��ֱ��BC�ϣ���ED=EC������BCE�Ƶ�C˳ʱ����ת60������ACF����EF����֤����AB=DB+AF��
�����̽����
��1����ͼ�ڣ������E���߶�AB���ӳ����ϣ������������䣬�߶�AB��DB��AF֮������������������ϵ����˵��������
��2�������E���߶�BA���ӳ����ϣ������������䣬����ͼ�۵Ļ����Ͻ�ͼ�β�����������д��AB��DB��AF֮���������ϵ������˵�����ɣ�

���𰸡������������֤������������������̽������1��AB=BD+AF����2��AF=AB+BD��
��������
��������������жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬������EAF=��BAC+��CAF=120�㣬��DBE=120�㣬��EAF=��DBE��Ȼ�����ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��AB=AE+BF������AB=DB+AF��
��1�������жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬������EFC=��FGC+��FCG����BAC=��FGC+��FEA����FCG=��FEA���ٸ�����FCG=��EAD����D=��EAD���ɵ���D=��FEA��Ȼ�����ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��EB=AF�������жϳ�AB=BD��AF���ɣ�
��2�����ȸ��ݵ�E���߶�BA���ӳ����ϣ���ͼ�۵Ļ����Ͻ�ͼ�β���������Ȼ���жϳ���CEF�ǵȱ������Σ������жϳ�EF=EC���ٸ���ED=EC���ɵ�ED=EF����CAF=��BAC=60�㣬���жϳ���DBE=��EAF����BDE=��AEF��������ȫ���������ж��ķ������жϳ���EDB�ա�FEA�������жϳ�BD=AE��EB=AF�������жϳ�AF=AB+BD���ɣ�
���������ED=EC=CF���ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF�����ECF=60�㣬��BCA=60�㣬BE=AF��EC=CF�����CEF�ǵȱ������Σ���EF=EC����CEF=60�㣬����ED=EC����ED=EF���ߡ�ABC�ǵ��������Σ���BCA=60�㣬���ABC�ǵȱ������Σ����CAF=��CBA=60�㣬���EAF=��BAC+��CAF=120�㣬��DBE=120�㣬��EAF=��DBE���ߡ�CAF=��CEF=60�㣬��A��E��C��F�ĵ㹲Բ�����AEF=��ACF������ED=EC�����D=��BCE����BCE=��ACF�����D=��AEF������EDB����FEA�У��ߡ�DBE=��EAF����D=��AEF��ED=EF��AAS�������EDB�ա�FEA����DB=AE��BE=AF����AB=AE+BE����AB=DB+AF��
��1��AB=BD+AF��
�ӳ�EF��CA���ڵ�G���ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF�����ECF=60�㣬BE=AF��EC=CF�����CEF�ǵȱ������Σ���EF=EC������ED=EC����ED=EF����EFC=��BAC=60�㣬�ߡ�EFC=��FGC+��FCG����BAC=��FGC+��FEA�����FCG=��FEA�����ߡ�FCG=��ECD����D=��ECD�����D=��FEA������ת�����ʣ��ɵ���CBE=��CAF=120�㣬���DBE=��FAE=60�㣬����EDB����FEA�У��ߡ�DBE=��EAF����D=��AEF��ED=EF��AAS�������EDB�ա�FEA����BD=AE��EB=AF����BD=FA+AB����AB=BD��AF��
��2����ͼ�ۣ���ED=EC=CF���ߡ�BCE�Ƶ�C˳ʱ����ת60������ACF�����ECF=60�㣬BE=AF��EC=CF��BC=AC�����CEF�ǵȱ������Σ���EF=EC������ED=EC����ED=EF����AB=AC��BC=AC�����ABC�ǵȱ������Σ����ABC=60�㣬���ߡ�CBE=��CAF�����CAF=60�㣬���EAF=180�㩁��CAF����BAC=180�㩁60�㩁60��=60�����DBE=��EAF����ED=EC�����ECD=��EDC�����BDE=��ECD+��DEC=��EDC+��DEC�����ߡ�EDC=��EBC+��BED�����BDE=��EBC+��BED+��DEC=60��+��BEC���ߡ�AEF=��CEF+��BEC=60��+��BEC�����BDE=��AEF������EDB����FEA�У��ߡ�DBE=��EAF����BDE=��AEF��ED=EF��AAS�������EDB�ա�FEA����BD=AE��EB=AF����BE=AB+AE����AF=AB+BD����AB��DB��AF֮���������ϵ�ǣ�AF=AB+BD��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=13cm��AC=20cm��BC���ϵĸ�Ϊ12cm�����ABC�����Ϊcm2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڡ�ABC�У�AD�Ǹߣ�AE��BF�ǽ�ƽ���ߣ������ཻ�ڵ�O����BAC=60�㣬��C=70�㣬���DAE����BOA�Ķ����� 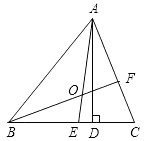
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ�AC=6cm��MB=10cm����M��N�ֱ�ΪAC��BC���е㣮![]()
��1�����߶�BC�ij���
��2�����߶�MN�ij���
��3����C���߶�AB�ӳ����ϣ�������AC��BC=b cm��M��N�ֱ����߶�AC��BC���е㣬���ܲ���MN�ij�������д����Ľ��ۣ�����Ҫ˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ͼ���ԭ���ϵľ�����2����λ���ȵĵ��ʾ�����ǣ� ��
A.2
B.2��-2
C.-2
D.����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ���к��۳���������ֱ����ԼΪ0.000 000 017m����ֱ�����ÿ�ѧ��������ʾΪ______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˵�Ǯ������10ԪǮ��20ԪǮ��50ԪǮ��ֽ�Ҹ�1�ţ��������ȡ��2��ֽ�ң�
��1����ȡ��ֽ�ҵ��ܶ���30Ԫ�ĸ��ʣ�
��2����ȡ��ֽ�ҵ��ܶ�ɹ���һ��51Ԫ����Ʒ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�Լˮ��Դ��ij�������վ����ͥ����ˮ��ʵ�н���ˮ�ۣ�ˮ�۷ֵ��������ƻ�ʹ��һ�����ڶ����͵�������ˮ�۷ֱ�ȫ�о����ͥ��80%��15%��5%��Ϊ����ȷ������֮��Ľ��ޣ��������˸���5�����ͥ��һ�������ˮ������λ��m3����������ͳ��ͼ����ͼ��ʾ�������ĸ��ƶϣ�������
������ˮ��������180m3�ĸ��о����ͥ����һ��ˮ�۽��ѣ�
������ˮ������240m3�ĸ��о����ͥ��������ˮ�۽��ѣ�
�۸��о����ͥ����ˮ������λ����150��180֮�䣻
�ܸ��о����ͥ����ˮ����ƽ����������180��
A.�٢�
B.�٢�
C.�ڢ�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ĸ����⣺���Խ����ഹֱƽ�ֵ��ı����������Σ����Խ����ഹֱ����ȵ��ı��������Σ����Խ�����ƽ������ȵ��ı����Ǿ��Σ����Խ�����ƽ�֡�����Ҵ�ֱ���ı����������Σ�����������ĸ����ǣ�������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com