
【题目】已知:如图,△ABC和△DBE均为等腰直角三角形. 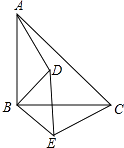
(1)求证:AD=CE;
(2)求证:AD和CE垂直.
【答案】
(1)证明:∵△ABC和△DBE是等腰直角三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=90°,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
即∠ABD=CBE,
在△ABD和△CBE中,
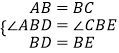 ,
,
∴△ABD≌△CBE(SAS),
∴AD=CE
(2)证明:延长AD分别交BC和CE于G和F,如图所示:
∵△ABD≌△CBE,
∴∠BAD=∠BCE,
∵∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,
又∵∠BGA=∠CGF,
∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,
∴∠AFC=∠ABC=90°,
∴AD⊥CE.
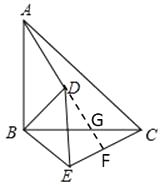
【解析】(1)由等腰直角三角形的性质得出AB=BC,BD=BE,∠ABC=∠DBE=90°,得出∠ABD=CBE,证出△ABD≌△CBE(SAS),得出AD=CE;(2)△ABD≌△CBE得出∠BAD=∠BCE,再由∠BAD+∠ABC∠∠BGA=∠BCE+∠AFC+∠CGF=180°,得出∠AFC=∠ABC=90°,证出结论.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
理解:
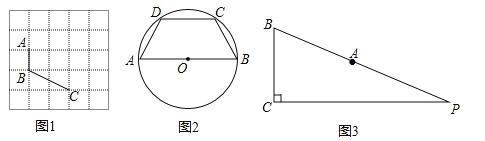
(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=![]() ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.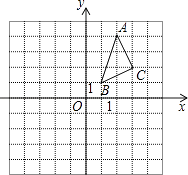
(1)作出△ABC关于x轴对称的△A1B1C1 , 并写出点C1的坐标;
(2)作出△ABC关于y对称的△A2B2C2 , 并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y= ![]() x的图象与一次函数y=kx﹣3的图象相交于点(2,a).
x的图象与一次函数y=kx﹣3的图象相交于点(2,a). 
(1)求a的值.
(2)求一次函数的表达式.
(3)在同一坐标系中,画出这两个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.![]()
(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com