
【题目】如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
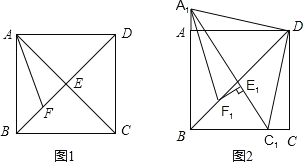
(1)求证:EF+![]() AC=AB;
AC=AB;
(2)点C1从点C出发,沿着线段CB向点B运动(不与点B重合),同时点A1从点A出发,沿着BA的延长线运动,点C1与A1的运动速度相同,当动点C1停止运动时,另一动点A1也随之停止运动。如图2,A1F1平分∠BA1C1,交BD于点F1,过点F1作F1E1⊥A1C1,垂足为E1,请猜想E1F1,![]() A1C1与AB三者之间的数量关系,并证明你的猜想;
A1C1与AB三者之间的数量关系,并证明你的猜想;
(3)在(2)的条件下,当A1E1=3,C1E1=2时,求BD的长。
【答案】(1)见解析;(2)见解析;(3)BD=![]()
【解析】
(1)过F作FM⊥AB于点M,首先证明△AMF≌△AEF,求出MF=MB,即可知道EF+![]() AE=AB.
AE=AB.
(2)连接F1C1,过点F1作F1P⊥A1B于点P,F1Q⊥BC于点Q,证明Rt△A1E1F1≌Rt△A1PF1,Rt△QF1C1≌Rt△E1F1C1后推出A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1化简为E1F1+![]() A1C1=AB.
A1C1=AB.
(3)设PB=x,QB=x,PB=1,E1F1=1,又推出E1F1+![]() A1C1=AB,得出BD=
A1C1=AB,得出BD=![]() .
.
(1)证明:如图1,过点F作FM⊥AB于点M,在正方形ABCD中,AC⊥BD于点E.
∴AE=![]() AC,∠ABD=∠CBD=45°,
AC,∠ABD=∠CBD=45°,
∵AF平分∠BAC,
∴EF=MF,
又∵AF=AF,
∴Rt△AMF≌Rt△AEF,
∴AE=AM,
∵∠MFB=∠ABF=45°,
∴MF=MB,MB=EF,
∴EF+![]() AC=MB+AE=MB+AM=AB.
AC=MB+AE=MB+AM=AB.
(2)E1F1, ![]() A1C1与AB三者之间的数量关系:E1F1+
A1C1与AB三者之间的数量关系:E1F1+![]() A1C1=AB
A1C1=AB
证明:如图2,连接F1C1,过点F1作F1P⊥A1B于点P,F1Q⊥BC于点Q,
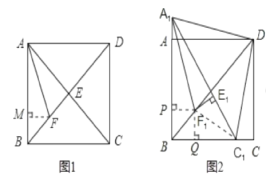
∵A1F1平分∠BA1C1,∴E1F1=PF1;同理QF1=PF1,∴E1F1=PF1=QF1,
又∵A1F1=A1F1,∴Rt△A1E1F1≌Rt△A1PF1,
∴A1E1=A1P,
同理Rt△QF1C1≌Rt△E1F1C1,
∴C1Q=C1E1,
由题意:A1A=C1C,
∴A1B+BC1=AB+A1A+BCC1C=AB+BC=2AB,
∵PB=PF1=QF1=QB,
∴A1B+BC1=A1P+PB+QB+C1Q=A1P+C1Q+2E1F1,
即2AB=A1E1+C1E1+2E1F1=A1C1+2E1F1,
∴E1F1+![]() A1C1=AB.
A1C1=AB.
(3)设PB=x,则QB=x,
∵A1E1=3,QC1=C1E1=2,
Rt△A1BC1中,A1B2+BC12=A1C12,
即(3+x)2+(2+x)2=52,
∴x1=1,x2=6(舍去),
∴PB=1,
∴E1F1=1,
又∵A1C1=5,
由(2)的结论:E1F1+![]() A1C1=AB,
A1C1=AB,
∴AB=![]() ,
,
∴BD=![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0)
(1)求证:无论m为任何非0实数,此方程总有两个实数根.
(2)若抛物线y=mx2+(1﹣5m)x﹣5(m≠0)与x轴交于A(x1,0)、B(x2,0)两点,且|x1﹣x2|=6,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
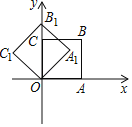
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市准备进一批每个进价为40元的小家电,经市场调查预测,售价定为50元时可售出400个;定价每增加1元,销售量将减少10个.
(1)设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)
(2)超市若准备获得利润6000元,并且使进货量较少,则每个应定价为多少元?
(3)超市若要获得最大利润,则每个应定价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() ,二次函数
,二次函数![]() 的对称轴为直线
的对称轴为直线![]() ,其图象过点
,其图象过点![]() 与
与![]() 轴交于另一点
轴交于另一点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数的解析式,写出顶点坐标;
(2)动点![]() 同时从
同时从![]() 点出发,均以每秒2个单位长度的速度分别沿
点出发,均以每秒2个单位长度的速度分别沿![]() 的
的![]() 边上运动,设其运动的时间为
边上运动,设其运动的时间为![]() 秒,当其中一个点到达终点时,另一个点也随之停止运动.连结
秒,当其中一个点到达终点时,另一个点也随之停止运动.连结![]() ,将
,将![]() 沿
沿![]() 翻折,若点
翻折,若点![]() 恰好落在抛物线弧上的
恰好落在抛物线弧上的![]() 处,试求
处,试求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(3)在(2)的条件下,Q为BN的中点,试探究坐标轴上是否存在点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,试说明理由.
的坐标;如果不存在,试说明理由.
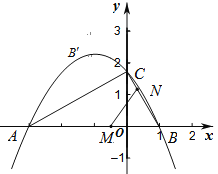
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
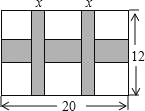
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
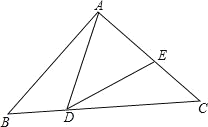
【题目】如图,在等腰△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=45°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BD为何值时AE取得最小值?
(3)在AC上是否存在点E,使△ADE是等腰三角形?若存在,求AE的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com