
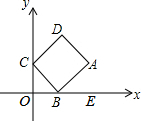
 如图,矩形ABCD的顶点A的坐标为(4,2),顶点B,C分别在x轴,y轴的正半轴上
如图,矩形ABCD的顶点A的坐标为(4,2),顶点B,C分别在x轴,y轴的正半轴上分析 (1)根据矩形的性质得出∠CBA=∠COB=90°,求出∠OCB+∠CBO=90°,∠CBO+∠ABE=90°,即可得出答案;
(2)过A作AF⊥x轴于F,证△COB∽△BFA,得出比例式,设OB=x,则BF=4-x,求出OC=-$\frac{1}{2}$x2+2x=-$\frac{1}{2}$(x-2)2+2,即可得出答案;
(3)求出n=-$\frac{1}{2}$(m-6)2+4,根据二次函数的性质得出即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠CBA=∠COB=90°,
∴∠OCB+∠CBO=90°,∠CBO+∠ABE=90°,
∴∠OCB=∠ABE;
(2)解:如图1,过A作AF⊥x轴于F,则∠COB=∠BFA=90°,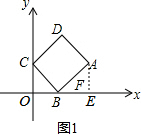
∵∠OCB=∠ABF,
∴△COB∽△BFA,
∴$\frac{CO}{BF}$=$\frac{OB}{AF}$,
∵A(4,2),
∴AF=2,OF=4,
设OB=x,则BF=4-x,
代入求出OC=-$\frac{1}{2}$x2+2x=-$\frac{1}{2}$(x-2)2+2,
∵C在y轴的正半轴上,
∴OC的范围是0<OC≤2;
(3)解:如图2,过D作DM⊥y轴于M,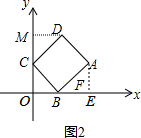
∵四边形ABCD是矩形,
∴∠DCB=90°,DC=AB,
∴∠DMC=∠DCA=90°,
∴∠MDC+∠MCD=90°,∠MCD+∠OCB=90°,
∴∠MDC=∠OCB=∠ABF,
在△DMC和△BFA中
$\left\{\begin{array}{l}{∠MDC=∠ABF}\\{∠DMC=∠AFB=90°}\\{DC=AB}\end{array}\right.$
∴△DMC≌△BFA,
∵D的坐标为(m,n),A(4,2),
设OB=x,BF=4-x,
∴MC=2,OM=n,DM=m=BF=4-x,
∴由(2)知:$\left\{\begin{array}{l}{n-2=-\frac{1}{2}(x-2)^{2}+2①}\\{m=4-x②}\end{array}\right.$
由②知:x=m-4,
代入①整理后得:n=-$\frac{1}{2}$(m-6)2+4,
∵m=4-x,B在x轴的正半轴上,n-2=-$\frac{1}{2}$(x+2)2+2,
∴0<m<4,2<n≤4,
∴当0<m<4时,n随m的增大而增大.
点评 本题考查了矩形的性质,二次函数的性质的应用,能根据题意得出二次函数的解析式是解此题的关键,题目比较好,难度偏大.


科目:初中数学 来源: 题型:解答题
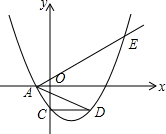 如图,抛物线y=$\frac{1}{{t}^{2}}$(x+t)(x-3t)交x轴负半轴于点A,交y轴于点C,点D,E均在抛物线上,且CD∥x轴,∠EAD=2∠ADC,求$\frac{AD}{AE}$的值.
如图,抛物线y=$\frac{1}{{t}^{2}}$(x+t)(x-3t)交x轴负半轴于点A,交y轴于点C,点D,E均在抛物线上,且CD∥x轴,∠EAD=2∠ADC,求$\frac{AD}{AE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
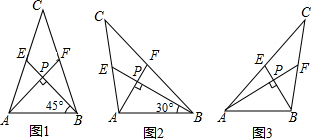
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
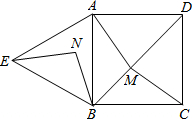 如图,△ABE是等边三角形,M是正方形ABCD对角线BD(不含B点)上任意一点,BM=BN,∠ABN=15°(点N在AB的左侧),当AM+BM+CM的最小值为$\sqrt{3}$+1时,正方形的边长为$\sqrt{2}$.
如图,△ABE是等边三角形,M是正方形ABCD对角线BD(不含B点)上任意一点,BM=BN,∠ABN=15°(点N在AB的左侧),当AM+BM+CM的最小值为$\sqrt{3}$+1时,正方形的边长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
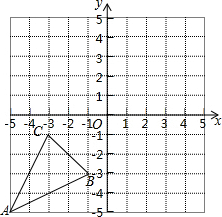 如图,在平面直角坐标系中,△ABC的顶点坐标是A(-5,5),B(-1,-3),C(-3.-1)
如图,在平面直角坐标系中,△ABC的顶点坐标是A(-5,5),B(-1,-3),C(-3.-1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com